HOW TO FIND AT WHICH POINT HORIZONTAL TANGENT CAN BE DRAWN

Problem 1 :

For what values of x does the graph of f(x) = (x² + 1) (x + 3) have horizontal tangent ?

Solution :

f(x) = (x² + 1) (x + 3)

From the given function, find the firs derivative to get the slope.

Since the functions are multiplied, we have to product rule to find the derivative.

Product rule :

d(uv) = uv' + vu'

u = (x² + 1) and v = x + 3

u' = 2x and v' = 1

f'(t) = (x² + 1) (1) + (x + 3) (2x)

= x² + 1  + 2x² + 6x

= 3x² + 6x + 1

Put f'(t) = 0

3x² + 6x + 1 = 0

Since this quadratic equation is not factorable, will use quadratic formula to solve it.

a = 3, b = 6 and c = 1

x = (-b ± √b² - 4ac)/2a

= (-6 ± √6² - 4(3)(1))/2(3)

= [-6 ± √(36 - 12)]/6

= [-6 ± √24]/6

= [-6 ± 2√6]/6

x = [-3 ± √6]/3

Hence the curve will have horizontal tangents at 

x = [-3 + √6]/3 and x = [-3 - √6]/3

Problem 2 :

Show that the tangents to the curve y = 7x³ + 11 at the points where x = 2 and x = – 2 are parallel.

Solution :

To find the tangent at the given points, we have to find the first derivative and apply the given x-coordinate. If we get the same results in both cases, we say that the tangents drawn at the points are parallel. Because parallel lines will have same slopes.

y = 7x³ + 11

dy/dx = 7(3x²) + 0

= 21x²

Since slopes are equal at x = -2 and x = 2, the tangents drawn at these points are parallel.

Problem 3 :

Find the points on the curve y = x³ at which the slope of the tangent is equal to the y-coordinate of the point.

Solution :

Let x -coordinate of the required point be p.

y-coordinate = y = p³

Slope of the tangent dy/dx = 3x²

Slope at x = p, dy/dx = 3p²

Given that,  slope of the tangent = y-coordinate of the point

3p² = p³

p³ - 3p² = 0

p²(p - 3) = 0

p = 0 and p = 3, then p = 3

If x = 0, y = 0

If x = 3, y = 3³  ==> 27

So, the required points are (0, 0) and (3, 27).

Problem 4 :

The home price index as percentage change from 2003 in year t, is represented by y = p(t)

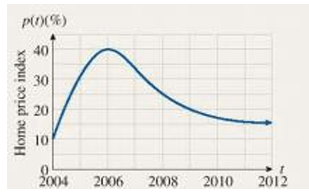
a) What year p'(t) = 0 ?

b) Is p'(2008) positive, negative or zero ?

c) Find the average rate of change from 2006 to 2008.

Solution :

a) By observing the graph given above, we can draw the horizontal tangent line at t = 2006.

b)  Observing the graph, after 2006 we see the curve is decreasing. It has negative slope. Then p'(2008) is negative.

c) At t = 2006, y = 40

At t = 2008, y = 25

Average rate of change = (25 - 40) / (2008 - 2006)

= -15/2

= -7.5

7.5% decreasing.

Problem 5 :

The position, in meters, of a body at time 𝑡 0 measured in seconds is

𝑠(𝑡) = t³ - 6t² - 36t

Find the body’s acceleration each time the velocity is zero.

Solution :

Given that, 𝑠(𝑡) = t³ - 6t² - 36t

s'(t) = 3t² - 6(2t) - 36(1)

s'(t) = 3t² - 12t - 36

When velocity is 0, then s'(t) = 0

3t² - 12t - 36 = 0

t² - 4t - 12 = 0

(t - 6)(t + 2) = 0

t = 6 and t = -2

To find the acceleration, we have to find the second derivative.

s''(t) = 3(2t) - 12(1)

= 6t - 12

Problem 5 :

Find the points on the curve

y = 2x³ + 3x² - 12x + 1

where the tangent is horizontal.

Solution :

y = 2x³ + 3x² - 12x + 1

dy/dx = 2(3x²) + 3(2x) - 12(1) + 0

= 6x² + 6x - 12

When we draw the horizontal tangent 

dy/dx = 0

6x² + 6x - 12 = 0

x² + x - 2 = 0

(x - 1)(x + 2) = 0

x = 1 and x = -2

At the points (1, -6) and (-2, 27), we draw the horizontal tangents.