HOW TO FIND AREA OF REGULAR HEXAGON

Find the perimeter area of each regular polygon. Leave your answer in simplest form.

Example 1 :

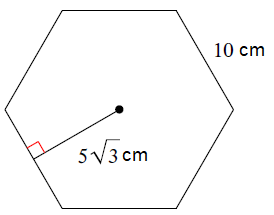
Solution :

Number of sides = 6

Perimeter of the shape = 6 x 10

= 60 cm

Perimeter = 60 cm

Length of apothem = 5√3 cm

Example 2 :

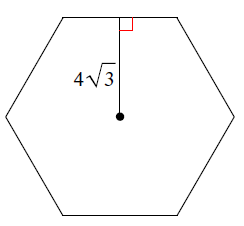
Solution :

Number of sides of a polygon = 6

by drawing lines from center to each vertex, we may draw six triangles of equal measure.

Angle measure of each triangle = 360/6 ==> 60

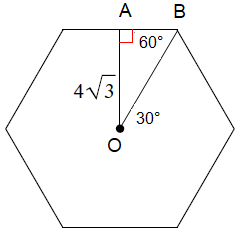
In triangle OAB,

OB = Hypotenuse, smaller side = AB

OB = 2(AB)

In special right triangle, the side which is opposite to 60 is √3(Smaller side).

OA = 4√3 then AB = 4 and OB = 2(4) ==> 8

Side length = 2(4) ==> 8

Example 3 :

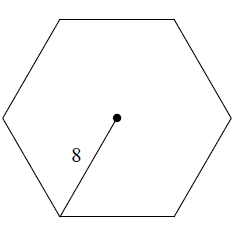
Solution :

Central angle of one triangle = 360/60

= 60 degree

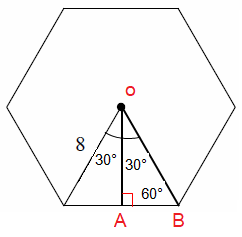
OB = 8, AB = Smaller side

2AB = OB, then AB = 4

OA = 4√3 (Apothem)

Side length = 8

Perimeter = 6(8) ==> 48

Area = (1/2) x 48 x 4√3

= 24 x 4√3

= 96√3 square units.

Example 4 :

(a) Find the perimeter of a rectangle whose length is 16 cm and width is 15 cm.

(b) What is the side length of a square whose perimeter is 38 cm?

(c) A regular pentagon’s side length is (x – 9) cm and perimeter is 45 cm. Find the value of x.

(d) A regular polygon’s perimeter is 45.5 m and side length is 3.5 m. Find the number of sides of the polygon.

Solution :

a)

Perimeter of rectangle = 2(length + width)

Length = 16 cm and width = 15 cm

Perimeter = 2(16 + 15)

= 2 (31)

= 62 cm

b) Perimeter of square = 38 cm

Let x be the side length of square

4x = 38

x = 38/4

x = 9.5 cm

c) 

Perimeter of regular pentagon = 45 cm

Number of sides for a pentagon = 5

Side length = x - 9

5(x - 9) = 45

x - 9 = 45/5

x - 9 = 9

x = 9 + 9

x = 18

(d) Let n be the number of sides of regular polygon.

Perimeter = 45.5 m

Side length = 3.5 m

3.5 n = 45.5

n = 45.5/3.5

n = 13

So, the required polygon has 13 sides.

Example 5 :

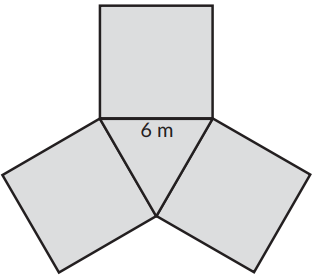
Find the perimeter of each figure. Each figure is made up of regular polygons only

a)

b)

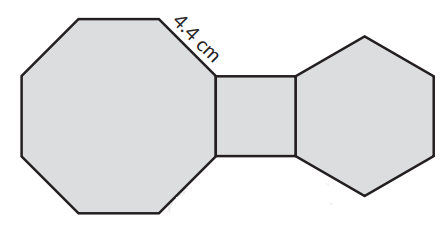
Solution :

a) the middle is a equilateral triangle surrounding with three squares.

Perimeter of triangle = 3(6)

= 18 m

In each square, we have to exclude one of the sides.

Perimeter of square = 13(6)

= 78 m

Perimeter of the shape = 18 + 78

= 96 m

b)

Perimeter of 8 sides polygon + Perimeter of square (excluding 2 sides) + Perimeter of hexagon

= 8(4.4) + 2(4.4) + 6(4.4)

= 35.2 + 8.8 + 26.4

= 70.4 m

Example 6 :

In the diagram of the base of the hexagonal pyramid, all the triangles are the same. Find the surface area of the hexagonal pyramid.

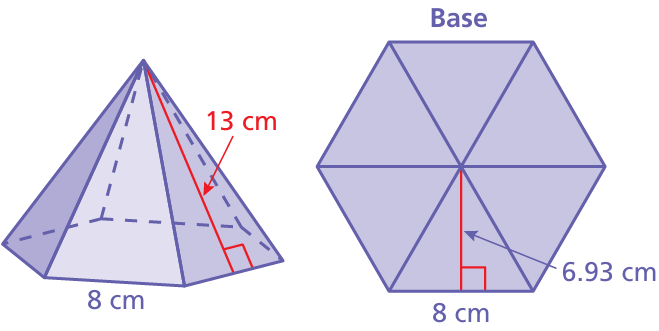
Solution :

Surface area of the hexagonal pyramid = base area + area around the figure

Base area = 1/2 x perimeter x apothem

perimeter = 6 (8)

= 48 cm

apothem = 6.93 cm

= (1/2) x 48 x 6.93

= 24 x 6.93

= 166.32 cm²

area around the figure = 6(area of triangle)

= 6(1/2) x 8 x 13

= 3 x 8 x 13

= 312 cm²

Surface area = 166.32 + 312

= 478.32 cm²

Example 7 :

ABCDEF is a regular hexagon if area of △ ABE is 100 sq cm find the side length of the hexagon.

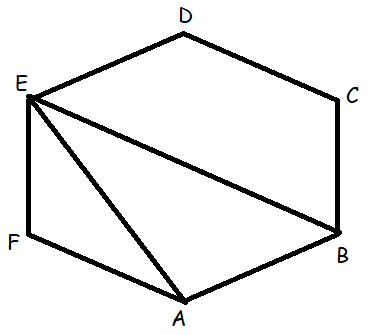
Solution :

Side lengths are equal. 

<EFA = [(6 - 2) x 180]/6

= (4/6) x 180

= 120

Then <FEA = <FAE  = 30

<EAB = 120 - 30 ==> 90

In triangle EAB, height of the triangle = AB and base of the triangle = EB

In 30-60-90 right triangle,

smaller side = AB, EB = 2 AB and EA = √3(AB)

Area of triangle = 100

(1/2) x EB x AB = 100

(1/2) x 2(AB) x AB = 100

AB²= 100

AB = 10 cm