HOW TO FIND HCF OF TWO NUMBERS

Find the highest common factor of the following numbers.

Problem 1 :

18, 48

Solution :

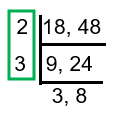
HCF (18, 48) = 2 × 3

= 6

Problem 2 :

30, 42

Solution :

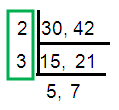
HCF (30, 42) = 2 × 3

= 6

Problem 3 :

18, 60

Solution :

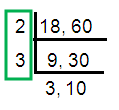
HCF (18, 60) = 2 × 3

= 6

Problem 4 :

27, 63

Solution :

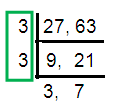
HCF (27, 63) = 3 × 3

= 9

Problem 5 :

36, 84

Solution :

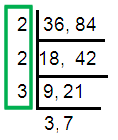
HCF (36, 84) = 2 × 2 × 3

= 12

Problem 6 :

34, 102

Solution :

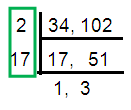
HCF (34, 102) = 2 × 17

= 34

Problem 7 :

The length of a big hall is 2000 cm and its breadth is 1600 cm. What would be the length of the longest tape that can be used to measure the length and breadth of the hall in an exact number of times?

Solution :

The length of a big hall  = 2000 cm

Breadth = 1600 cm

To find the length of the longest tape that can be used to measure the length and breadth, we need to find the common measure for both length and breadth.

Since the common measure should be the largest, we find highest common factor.

HCF (2000, 1600) = 2 × 2 × 2 × 2 × 5 × 5

= 400 cm

Problem 8 :

A hall 33 m long and 16 m wide is to be paved with square floor tiles. What would be the length of the largest tile that can be used such that the entire floor is covered?

Solution :

Length of the hall = 33 m

Width of the hall = 16 m

To find length of the largest tile that can be used, we find the highest common factor of 33 and 16.

There is no common divisor for 33 and 16. So, highest common factor is 1.

1 m length of square tile is needed to cover the hall.

Problem 9 :

What is the maximum number of equal squares of the biggest possible size that can be cut out of a piece of cardboard 48 cm broad and 64 cm long? what would be the length of each square?

Solution :

Length of the cardboard = 64 cm

Width of the card board = 48 cm

Length of square to be cut out.

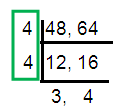
HCF (48, 64) =  16

Therefore the length of each square = 16 cm

Problem 10 :

Two bags of wheat contain 42 kg and 56 kg of wheat, respectively. What is the greatest weight that can be used to measure the wheat in each bag an exact number of times ? How many times will it take to weigh all the wheat in the two bags using this weight ?

Solution :

Weight of one bag = 42 kg

Weight of another bag = 56 kg

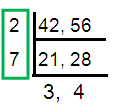
HCF (42, 56) =  14

So, the greatest weight that can be used to measure the wheat in two bags is 14.

Number of time they can measure from the first bag :

= 42/14

= 3 times from the first bag

Number of time they can measure from the second bag :

= 56/14

= 4 times from the second bag

= 3 + 4

= 7

So, the required number of time is 7.

Problem 11 :

The ratio of two numbers is 3 : 4 and their HCF is 4. Their LCM is

a)  12    b)  16      c)  24     d) 48

Solution :

The numbers are in the ratio is 3 : 4.

The two numbers are 3x and 4x.

Given that HCF is 4.

3x ==> 3(4) ==> 12

4x ==> 4(4) ==> 16

LCM of 12 and 16.

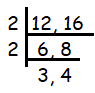
LCM = 2 x 2 x 3 x 4

= 48

Problem 12 :

The sum of two numbers is 216 and their HCF is 27. The numbers are :

a)  27, 189    b)  81, 189     c)  108, 108     d) 154, 162

Solution :

Let x and y be the two numbers.

x + y = 216

HCF = 27

27x and 27y are two original numbers

27x + 27y = 216

(x + y) = 216/27

x + y = 8

The two co-prime and their sum is 8,

(1, 7) and (3, 5)

27(1) ==> 27

27(7) ==> 189

27(3) ==> 81

27(5) ==> 135

So, option a is correct.

Problem 13 :

The sum of two numbers is 528 and their HCF is 33. The number is pairs of numbers satisfying the above conditions is :

a)  4      b)  6       c)  8      d)  12

Solution :

33x and 33y are two required numbers since their HCF is 33.

33x + 33y = 528

x + y = 528/33

x + y = 16

Two co-primes with the sum 16 are (1, 15) (3, 13) (5, 11) (7, 9)

(33, 495)(99, 429) (165, 363)(231, 297)

So, there are 4 pairs.