HOW TO FIND HCF OF THREE NUMBERS

Find the least common multiple using ladder method.

Problem 1 :

70, 105, 175

Solution :

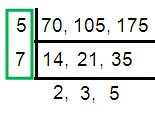
HCF (70, 105, 175) = 5 × 7

= 35

Problem 2 :

91, 112, 49

Solution :

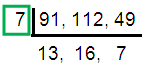
HCF (91, 112, 49) =  7

Problem 3 :

18, 54, 81

Solution :

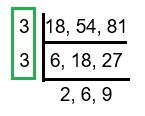
HCF (18, 54, 81) =  9

Problem 4 :

12, 45, 75

Solution :

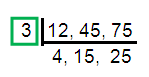
HCF (12, 45, 75) =  3

Problem 5 :

The sum of two numbers is 528 and their HCF is 33. The number of pairs of numbers satisfying the above conditions is 

a)  4      b)  6     c)  8     d)  12

Solution :

HCF of two numbers is 33, let the numbers be 33a and 33b

Sum of these two numbers = 528

33a + 33b = 528

a + b = 528/33

a + b = 16

Now co-primes are whose sum 16 are

(1, 15) (3, 13) (5, 11) (7, 9) 

So 4 pairs, option a is correct.

Problem 6 :

The number of number pairs lying between 40 and 100 with thier HCF as 15 is 

a)  3      b)  4     c)  5     d)  6

Solution :

Let 15a and 15b are two numbers

Multiples of 15 lies between 40 and 100 are

45, 60, 75, 90

(45, 60) (45, 75) (45, 90) (60, 75) (60, 90) (75, 90)

• HCF of 60 and 90 is 30
• HCF of 45 and 90 is 45
• HCF of (45, 60) (45, 75) (60, 75) (75, 90) is 15.

So, option b is correct.

Problem 7 :

The HCF of two numbers is 12 and their difference is 12. The numbers are 

a)  66, 78      b)  70, 82     c)  94, 106    d)  84, 96

Solution :

Let 12a and 12b are two numbers

Difference = 12

12a - 12b = 12

12(a - b) = 12

a - b = 12/12

a - b = 1

Option a :

66 = 3 x 2 x 11

78 = 2 x 3 x 13

HCF = 2

Option b :

70 = 2 x 5 x 7

82 = 2 x 41

HCF = 2

Option c :

94 = 2 x 47

106 = 2 x 53

HCF = 2

Option d :

84 = 2 x 2 x 3 x 7

96 = 2 x 2 x 2 x 2 x 2 x 3

HCF = 2 x 2 x 3

= 12

84 = 12(7)

96 = 12(8)

Here a = 8 and b = 7

a - b = 8 - 7 

= 1

So, option d is correct.

Problem 8 :

The product of two numbers is 4107. IF the HCF of these numbers is 37, then the greater number is 

a)  101      b)  107     c)  111     d)  185

Solution :

HCF of two numbers is 37. Let the numbers be 37a and 37b

Product of two numbers = 4107

37a (37b) = 4107

a x b = 4107/(37 x 37)

a x b = 3

a = 1 and b = 3

37a ==> 37(1) ==> 37

37b ==> 37(3) ==> 111

The required numbers are 37 and 111. So, the greater number is 111. Option c is correct.

Problem 9 :

The product of two numbers is 1320 if their HCF is 6. The LCM of the numbers is 

a)  220      b)  1314     c)  1326     d) 7920

Solution :

HCF of two numbers is 6. Let the numbers be 6a and 6b

Product of two numbers = 1320

Product of two numbers = LCM x HCF

1320 = LCM x 6

1320/6 = LCM

LCM = 220

Option a is correct.

Problem 10 :

The HCF and LCM of two numbers are 50 and 250 respectively. If the first number is divided by 2, the quotient is 50. The second number is :

a)  50      b)  100     c)  125     d) 250

Solution :

HCF = 50

LCM = 250

Product of LCM and HCF = 50 x 250

= 12500

When dividing the first number by 2, we get quotient as 50. Then, the number is 50 x 2 which is 100.

The first number = 100

The second number = 12500/100

= 125

So, the second number is 125. Option c is correct.

Problem 11 :

The greatest number which can divide 1356, 1868 and 2764 leaving the same remainder 12 in each case is :

a)  64      b)  124     c)  156     d) 260

Solution :

1356 - 12 ==> 1344

1868 - 12 ==> 1856

2764 - 12 ==> 2752

HCF of 1344, 1856 and 2752

HCF = 2 x 2 x 2 x 2 x 2 x 2

= 64

So, the required greatest number is 64.