HOW TO DETERMINE IF THE TABLE REPRESNTS DIRECT VARIATION

Definition of direct variation :

Two quantities x and y show direct variation when

y = kx

where k is a number and k ≠ 0.

How to determine if the table represents direct variation ?

• Take the inputs as x and outputs as y.
• Find the value of constant of variation (k) = y/x
• If constant of variation is the same, then we can say the table represents the direct variation.

Meaning of direct variation :

As x increases, y increases by the same factor. As x decreases, y decreases by the same factor.

The cost of items is directly proportional to the number of items.

Direct variation on graph :

The graph is a straight line that passes through the origin.

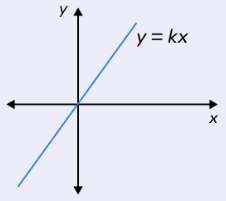
Tell whether x and y show direct variation. Explain your reasoning.

Problem 1 :

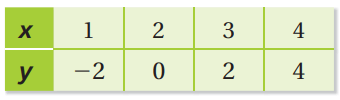
Solution :

Since the constant of variation is not same, the table does not represent direct variation. For more understanding, plotting the points in the graph,

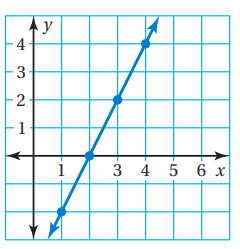
Observing the graph, it doesn't pass through origin. So, it is not direct variation.

Problem 2 :

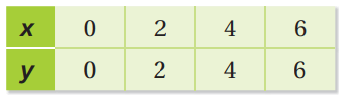
Solution :

Here x = 0, y = 0. It passes through origin.

Constant variation k = y/x

Since constant of variation is the same, it represents direct variation.

By plotting all the points in the graph, we get

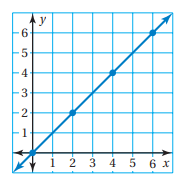
By observing the graph, it passes through the origin. The table represents direct variation.

Problem 3 :

Solution :

From the table, when input x = 0, y is not equal to 0.

When x = 1, y = 1, then k = y/x = 1

When x = 2, y = 4, then k = y/x = 4/2 ==> 2

When x = 3, y = 7, then k = y/x = 7/3

The constant of variation is not the same. Then the table does not represent the direct variation.

Problem 4 :

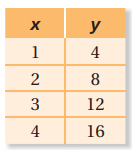
Solution :

When x = 1, y = 4, then k = y/x = 4/1 ==> 4

When x = 2, y = 8, then k = y/x = 8/2 ==> 4

When x = 3, y = 12, then k = y/x = 12/3 ==> 4

When x = 4, y = 16, then k = y/x = 16/4 ==> 4

The constant of variation is same. Then the table represents the direct variation.

Problem 5 :

Solution :

When x = -2, y = 4, then k = y/x = 4/(-2)==> -2

When x = -1, y = 2, then k = y/x = 2/(-1) ==> -2

It passes through origin.

When x = 1, y = 2, then k = y/x = 2/1 ==> 2

Even though it passes through origin, its constant of variation is not the same. So, the table does not represent direct variation.

Problem 6 :

The table shows the profit y for recycling x pounds of aluminum. Tell whether x and y show direct variation.

Solution :

Since the constant of variation is the same, it represents direct variation.

Problem 7 :

Describe and correct the error in telling whether x and y show direct variation

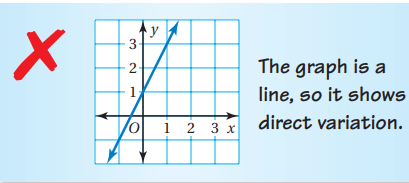
Solution :

Even though it is a straight line, it does not pass through the origin. It is not a direct variation.

Problem 8 :

Tell whether x and y show direct variation. If so, write an equation of direct variation

Solution :

If x = 500, y = 40, then k = y/x = 40/500 ==> 0.08

If x = 700, y = 50, then k = y/x = 50/700 ==> 0.071

Since the constant of variation is not same, it is not a direct variation.