HOW TO DETERMINE IF A TABLE REPRESENTS DIRECT VARIATION

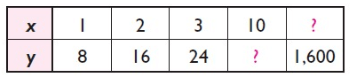
Problem 1 :

The table gives pairs of values for the variables x and y.

a) Show that one variable varies directly as the other.

b) Find the constant of variation by comparing as the other.

c) Express the relationship between the variables as a formula.

d) Find the values missing in the table.

Solution :

a.

b.

y = kx

k = y/x

k = 8/1

Constant of variation is k = 8

c.

y = kx

k = y/x

d.

 x = 1 and y = 8

y = kx

8 = k

y = 8x

If x = 10 and y =?

y = 8x

y = 8(10)

y = 80

if x =? And y = 1600

y = 8x

1600 = 8x

x = 1600/8

x = 200

Tell, in each case, whether one variable directly as the other. If it does, express the in between the variables by means of a formula.

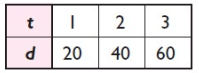
Problem 2  :

Solution :

Write an equation that represents the relationship given in the table above.

y = 20x

d = 20t

Each ‘d’ value is 20 times the corresponding ‘t’ value.

This is a direct variation.

Because the equation y = 20x is in the form of y = kx, where k = 20

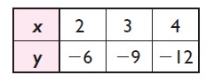
Problem 3 :

Solution :

Write an equation that represents the relationship given in the table above.

y = -3x

Each y value is -3 times the corresponding x value

This is a direct variation.

Because the equation y = -3x is in the form of y = kx, where k = -3

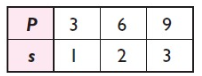
Problem 4 :

P directly varies to s.

Problem 5 :

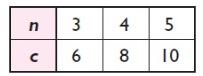
Solution :

n directly varies to c.

Problem 6 :

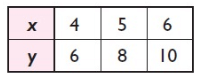
Solution :

We don't have direct variation between x and y.