HOW TO CHECK IF THE TWO CIRCLES DOES NOT INTERSECT

Consider two circles with radii r₁ and r₂

Let d be the distance between the centers of the two circles.

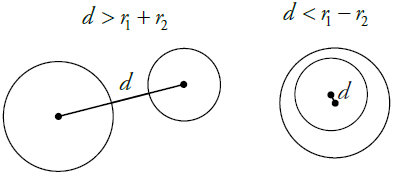
Problem 1 :

Circle P has center (−4, −1) and radius 2 units, circle Q has equation x² + y² − 2x + 6 y + 1 = 0. Show that the circles P and Q do not touch

Solution :

Center of the circle P = (-4, -1)

Center of the circle with Q :

x² + y² − 2x + 6 y + 1 = 0

x² − 2x + y² + 6 y + 1 = 0

(x - 1)² + (y + 3)² - 1² - 3² + 1 = 0

(x - 1)² + (y + 3)² = 9

Center of Q (1, -3) and radius = 3

Distance between P and Q = √(1 + 4)² + (-3 + 1)²

= √5² + (-2)²

= √(25 + 4)

Distance between two centers = √29

r₁ = 2, r₂ = 3

r₁ + r₂ = 2 + 3 ==> 5

√29 > 5

Distance between centers > sum of radii

Problem 2 :

A circle R has equation x² + y² - 2x - 4y - 4 = 0 and circle S has equation

(x - 4)² + (y - 6)² = 4

show that the circles R and S touch externally.

Solution :

To prove the two circles are touching each other externally, we have to find the center of two circle.

Distance between two centers = Radius of circle R + radius of circle S

Finding center of the circle R :

x² + y² - 2x - 4y - 4 = 0

x² - 2x + y² - 4y - 4 = 0

x² - 2x(1) + 1² - 1² + y² - 2y(2) + 2² - 2² - 4 = 0

(x - 1)² - 1 + (y - 2)² - 4 - 4 = 0

(x - 1)² + (y - 2)² - 9 = 0

(x - 1)² + (y - 2)² = 9

Center of the circle R is (1, 2) and radius = 3

Finding center of the circle S :

(x - 4)² + (y - 6)² = 4

Center of the circle S is (4, 6) and radius = 2

Distance between two centers :

= √(x₂ - x₁)² + (y₂ - y₁)² 

= √(4 - 1)² + (6 - 2)² 

= √3² + 4² 

= √(9 + 16)

= √25

= 5

Sum of radii = 3 + 2

= 5

So, the circles are touching each other externally.

Problem 3 :

Three touching circles have their centers A, B and C of the same horizontal line.

The diameter of the circle, center B is 10 and the circle, center C has diameter 2.

If the equation of the circle center A is x² + y² + 6x - 12y + 41 = 0, find the equations of the other two circles.

Solution :

Diameter of the circle B = 10, radius = 5 units

Diameter of circle C = 2 units, radius = 1 unit.

Equation of circle A :

x² + y² + 6x - 12y + 41 = 0

x² + 6x + y² - 12y + 41 = 0

(x + 3)² - 3² + (y - 6)² - 6² + 41 = 0

(x + 3)² - 9 + (y - 6)² - 36 + 41 = 0

(x + 3)² + (y - 6)² - 45 + 41 = 0

(x + 3)² + (y - 6)² - 4 = 0

(x + 3)² + (y - 6)²  = 4

Center is (-3, 6) and radius = 2

From the picture above, it is clear the circles are touching each other externally and y-coordinates of center of each circle will be the same.

Let (x, y) be the center of the circle B.

√(x₂ - x₁)² + (y₂ - y₁)² = radius of circle A + radius of the circle B

√(x + 3)² + (6 - 6)² = 2 + 5

√(x + 3)² = 7

x + 3 = 7

x = 7 - 3

x = 4

So, center of the circle B is (4, 6) with radius 5 units.

Equation of circle B: 

(x - h)² + (y - k)² = r²

(x - 4)² + (y - 6)² = 5²

x² - 8x + 16 + y² - 12y + 36 = 25

x² - 8x + y² - 12y + 36 + 16 = 25

x² + y²  - 8x - 12y + 27 = 0

Equation of circle C: 

Let (x, y) be the center of the circle B.

√(x₂ - x₁)² + (y₂ - y₁)² = radius of circle B + radius of the circle C

√(x - 4)² + (6 - 6)² = 5 + 1

√(x - 4)² = 6

x - 4 = 6

x = 6 + 4

x = 10

Center of the circle C is (10, 6) and radius = 1 unit.

(x - 10)² + (y - 6)² = 1²

x² - 20x + 100 + y² - 12y + 36 = 1

x² - 20x + y² - 12y + 136 - 1 = 0

x² + y²  - 20x - 12y + 135 = 0