HONORS GEOMETRY PRACTICE PROBLEMS IN SPECIAL RIGHT TRIANGLES

Problem 1 :

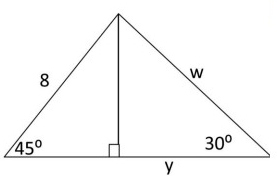
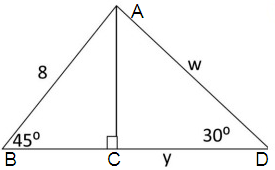
Solution :

Let x be the shorter length.

AC = BC

Hypotenuse = 2 ⋅ shorter length

8 = 2 ⋅ BC

BC = 8/2

BC = 4 = AC

Finding the value of w :

Hypotenuse = 2 ⋅ shorter length

In triangle ACD, AC is the smaller side.

Here, hypotenuse = w, and AC = 4

w = 2 ⋅ 4

w = 8

So, the value of w is 8.

Finding the value of y :

longer length = √3 ⋅ shorter length

Here, CD = y, and shorter length = 4.

y = √3 ⋅ 4

y = 4√3

So, the value of y is 4√3.

Problem 2 :

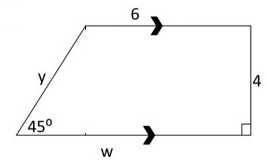
Solution :

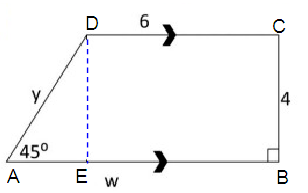
CB = DE = 4

Finding the value of y :

(AD)² = (AE)² + (ED)²

y² = 4² + 4² 

y² = 32

y = √32

y = 4√2

So, the value of y is 4√2.

Finding the value of w :

AB = AE + EB

w = 4 + 6

w = 10

So, the value of w is 10.

Problem 3 :

What is the perimeter of square SQRE ?

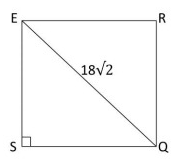
Solution :

By observing the figure,

∠ESQ is a 45º - 45º - 90º triangle.

let x be the side length.

By using Pythagorean theorem.

(EQ)² = (ES)² + (SQ)²

(18√2)² = x² + x²

324 ⋅ 2 = 2x²

648 = 2x²

648/2 = x²

324 = x²

√324 = x

18 = x

Perimeter of square = 4 ⋅ x

18 ⋅ 4 = 72

So, the perimeter of the square is 72.

Problem 4 :

What is the area of this triangle ?

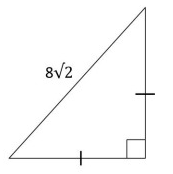
Solution :

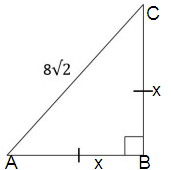
let x be the side length.

By using Pythagorean theorem.

(AC)² = (AB)² + (BC)²

(8√2)² = x² + x²

64 ⋅ 2 = 2x²

128 = 2x²

128/2 = x²

64 = x²

8 = x

Area of the triangle = 1/2 b ⋅  h

= 1/2 (8) ⋅ 8

= 32

So, area of the triangle is 32.

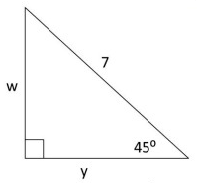
Problem 5 :

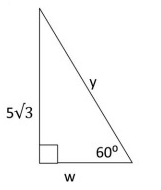
Solution :

Finding the value of w :

By 30º - 60º - 90º triangle theorem,

longer length = √3 ⋅ shorter length

Here, longer length = 5√3, and shorter length = w.                                                                                     

5√3 = √3 ⋅ w

w = 5√3/√3

So, the value of w is 5.

Finding the value of y :

By 30º - 60º - 90º triangle.

Hypotenuse = 2 ⋅ shorter length

Here, hypotenuse = y, and shorter length = w.

y = 2 ⋅ 5

y = 10

So, the value of y is 10.

Problem 6 :

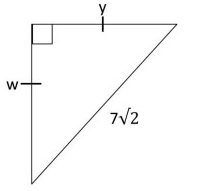
Solution :

w and y be the side length.

Let x be the side length.

By using Pythagorean theorem.

(CB)² = (AB)² + (AC)²

(7√2)² = x² + x²

49 ⋅ 2 = 2x²

98 = 2x²

98/2 = x²

49 = x²

7 = x

So, the values of w and y is 7.

Problem 7 :

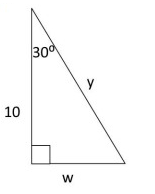
Solution :

Finding the value of w :

By 30º - 60º - 90º triangle theorem,

longer length = √3 ⋅ shorter length

Here, longer length = 10, and shorter length = w.                                                                                     

10 = √3 ⋅ w

w = 10/√3

So, the value of w is 10/√3.

Finding the value of y :

By 30º - 60º - 90º triangle.

Hypotenuse = 2 ⋅ shorter length

Here, hypotenuse = y, and shorter length = w.

y = 2 ⋅ 10/√3

y = 20/√3

So, the value of y is 20/√3.

Problem 8 :

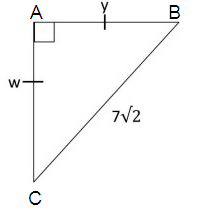
Solution :

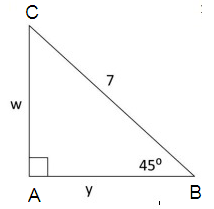
w and y be the side length.

Let x be the side length.

By using Pythagorean theorem.

(CB)² = (AB)² + (AC)²

7² = x² + x²

49 = 2x²

49/2 = x²

Squaring on each sides.

√(49/2) = √x²

7/√2 = x

So, the values of w and y is 7/√2.

Problem 9 :

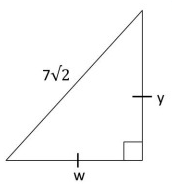
Solution :

w and y be the side length.

Let x be the side length.

By using Pythagorean theorem.

(AC)² = (AB)² + (BC)²

(7√2)² = x² + x²

49 ⋅ 2 = 2x²

98 = 2x²

98/2 = x²

49 = x²

7 = x

So, the values of w and y is 7.

Problem 10 :

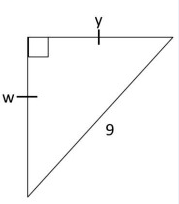
Solution :

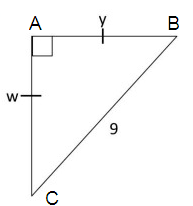
w and y be the side length.

Let x be the side length.

By using Pythagorean theorem.

(BC)² = (AB)² + (AC)²

9² = x² + x²

81  = 2x²

81/2 = x²

Squaring on each sides.

√(81/2) = √x²

9/√2 = x

So, the values of w and y is 9/√2 .