Learn Math step-by-step
GRAPHING TANGENT FUNCTIONS WITH TRANSFORMATIONS WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
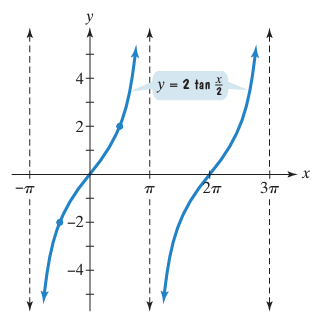
Graph y = 2 tan (x/2) for -π < x < 3π
Problem 2 :
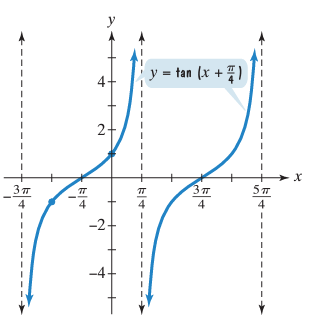
Graph two full periods of y = tan (x + π/4)
Problem 3 :
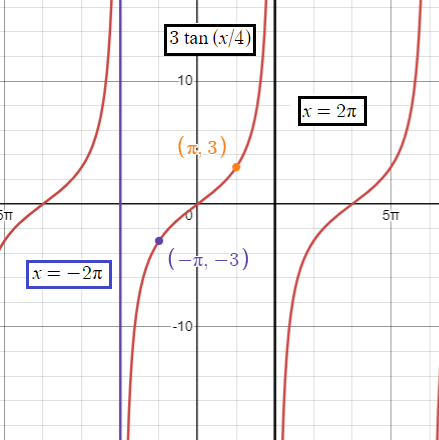
Graph two full periods of y = 3 tan (x/4)
Problem 4 :
Graph two full periods of y = (1/2) tan (2x)
Problem 5 :
Graph two full periods of y = -2 tan (x/2)
Answer Key
1)
- Thus two consecutive asymptotes occur at x = -𝜋 and x = 𝜋.
- An x-intercept is 0 and the graph passes through (0, 0).
- So, the required points on the curve are (-𝜋/2, -2) and (𝜋/2, 2).
x = 𝜋(2k + 1)
- When k = -1, x = -𝜋
- When k = 0, x = 𝜋
- When k = 1, x = 3𝜋
- When k = 2, x = 5𝜋
2)
- Thus two consecutive asymptotes occur at x = -3𝜋/4 and x = 𝜋/4.
- x-intercept is at (-𝜋/4, 0)
- the required points are (-𝜋/2, -1) and (0, 1).
x = 𝜋(k + 1/4)
- When k = -1, x = -3𝜋/4
- When k = 0, x = 𝜋/4
- When k = 1, x = 5𝜋/4
- When k = 2, x = 9𝜋/4
3)
- Thus two consecutive asymptotes occur at x = -2𝜋 and x = 2𝜋.
- x-intercept is at (0, 0) at the interval (-2𝜋, 2𝜋).
- the required points are (-𝜋, -3) and (𝜋, 3).
x = 2𝜋(2k + 1)
- When k = -1, x = -3𝜋/4
- When k = 0, x = 𝜋/4
- When k = 1, x = 5𝜋/4
- When k = 2, x = 9𝜋/4
4)
- Thus two consecutive asymptotes occur at x = -𝜋/4 and x = 𝜋/4.
- x-intercept is at 0
- the required points are (-𝜋/8, -0.5) and (𝜋/8, 0.5).
x = (1/4)𝜋(2k + 1)
- When k = -1, x = -𝜋/4
- When k = 0, x = 𝜋/4
- When k = 1, x = 3𝜋/4
- When k = 2, x = 5𝜋/4
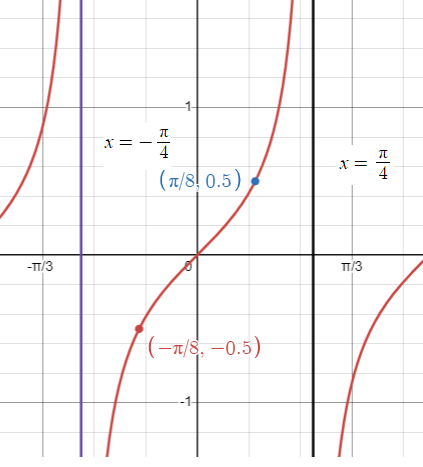
5)
- Thus two consecutive asymptotes occur at x = -𝜋 and x = 𝜋.
- x-intercept is 0
- the required points are (-𝜋/2, -2) and (𝜋/2, 2).
x = 𝜋(2k + 1)
- When k = -1, x = -𝜋
- When k = 0, x = 𝜋
- When k = 1, x = 3𝜋
- When k = 2, x = 5𝜋
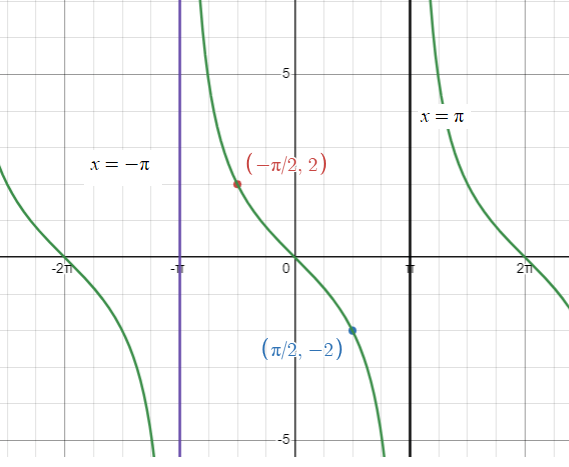
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling