GRAPHING STEP FUNCTIONS

A step function or staircase function is a piecewise function containing all constant "pieces".

The constant pieces are observed across the adjacent intervals of the function, as they change value from one interval to the next.

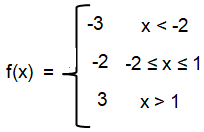
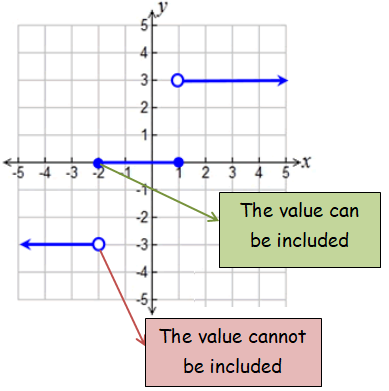
A step function is discontinuous cannot draw a step function without removing your pencil from your paper

Note :

It may be or may not be a function. To check whether it is a function, we have to use vertical line test.

Graph the following step functions :

Problem 1 :

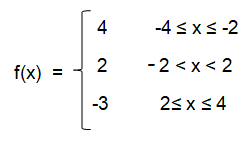
Solution :

f(x) = y

So, the line that we draw should be horizontal line. It will pass through the point 4, 2 and -3 respectively. 

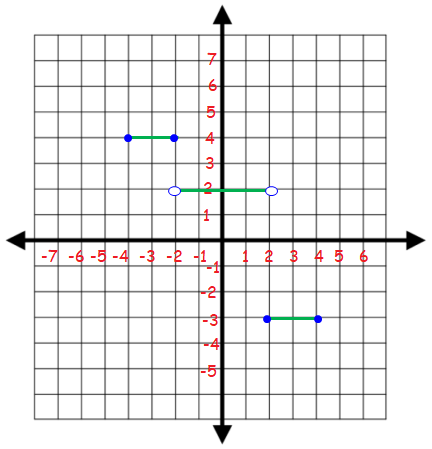
For y = 4, the domain is [-4, -2]. At both ends, we should use the filed circle.

For y = 2, the domain is (-2, 2). At both ends, we should use the empty circle.

For y = -3, the domain is [4, 4]. At both ends, we should use closed circles.

Problem 2 :

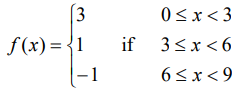
Solution :

f(x) = y

So, the line that we draw should be horizontal line. It will pass through the point 3, 1 and -1 respectively. 

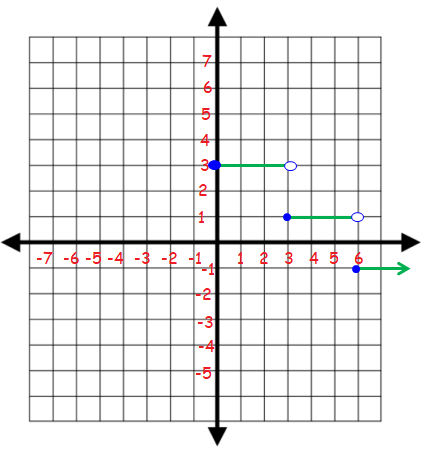
For y = 3, the domain is [0, 3). At the left end use filled circle and at right end use unfilled circle.

For y = 1, the domain is [3, 6). At the left end use filled circle and at right end use unfilled circle.

For y = 1, the domain is [6, 9). At the left end use filled circle and at right end use unfilled circle.

Problem 3 :

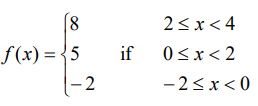
Solution :

f(x) = y

So, the line that we draw should be horizontal line. It will pass through the point 8, 5 and -2 respectively. 

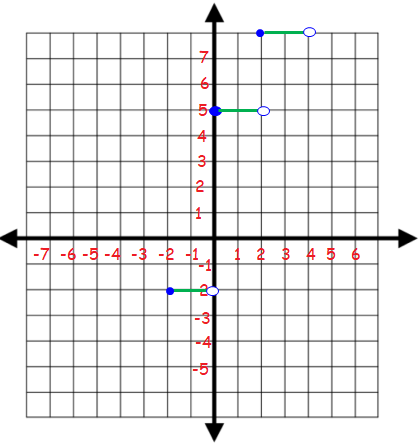
For y = 8, the domain is [2, 4). At the left end use filled circle and at right end use unfilled circle.

For y = 5, the domain is [0, 2). At the left end use filled circle and at right end use unfilled circle.

For y = -2, the domain is [-2, 0). At the left end use filled circle and at right end use unfilled circle.

Problem 4 :

The charge to rent a jet ski is $2.00 for the first hour and $1.00 for each additional hour or fraction there of. The fee is a function of the time the jet ski is used.

a) Sketch the graph of a step function that models this cost.

b) Write an equation for the linear function that approximates the cost. Sketch the graph of this linear function.

Solution :

a)  The initial payment is $2. 

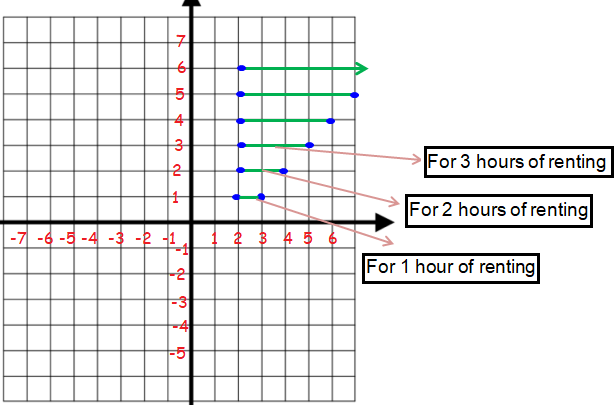
b)  Initial cost = $2.

Let x be the number of hours renting.

Total cost = y

y = 2 + 1x

y = x + 2

Problem 5 :

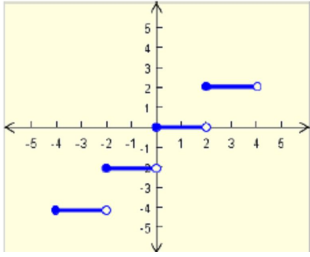
Solution :

Observing the graph from left to right, the first least value is -4.

From bottom to top,

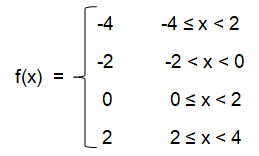
Problem 6 :

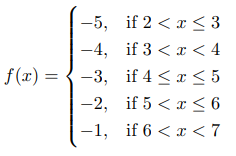
(a) Domain of f

(b) Range of f

(c) f(2)

(d) f(3)

(e) f(7)

(f) f(3.18)

(g) f(√ 20.14)

Solution :

(a) Domain of f = (2, 7)

(b) Range of f = {-5, -4, -3, -2, -1}

(c) f(2) does not exists

(d) f(3) = -5

(e) f(7) does not exists.

(f) f(3.18)

3.18 lies between 3 to 4. So, the value of f(3.18) is -4.

(g) f(√20.14)

√20.14 = 4.48 and lies between 4 to 5. So, the value of  f(√20.14) is -3.