GRAPHING SQUARE ROOT FUNCTIONS

Graph each of the function given below.

Example 1 :

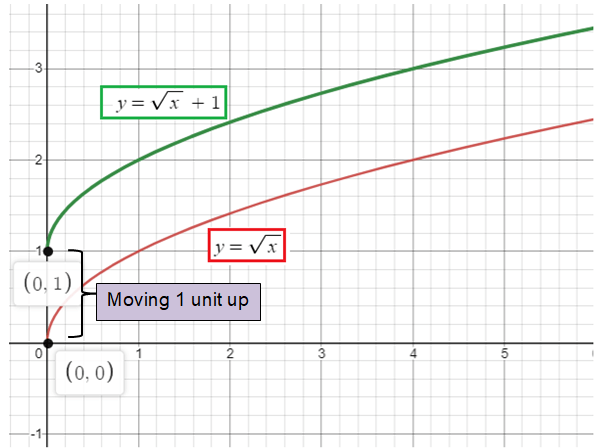
y = √x + 1

Solution :

By considering the parent function y = √x

1 is added along with the parent function, so there is vertical translation. We have to move the graph 1 unit up.

Example 2 :

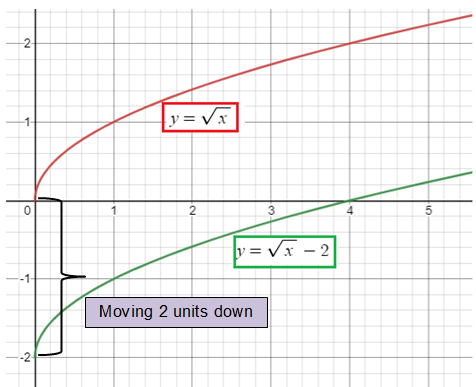
y = √x - 2

Solution :

By considering the parent function y = √x

2 is subtracted from the parent function, so there is vertical translation. We have to move the graph 2 units down.

Example 3 :

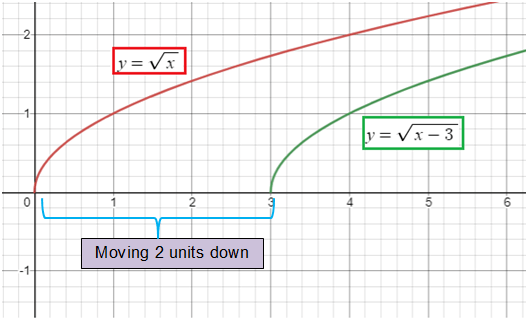
y = √(x - 3)

Solution :

By considering the parent function y = √x

3 is subtracted from x, so there will be a horizontal translation.

We have to move the graph, 3 units to the right.

Example 4 :

y = 3√(x + 1) + 4

Solution :

By considering the parent function y = √x

1 is added with x, so we have to perform horizontal translation. Move the graph 1 unit to the left.

4 is added with the parent function, so we have to perform vertical translation. Move the graph 4 units up.

3 is multiplied with the parent function, we have to stretch 3 units.

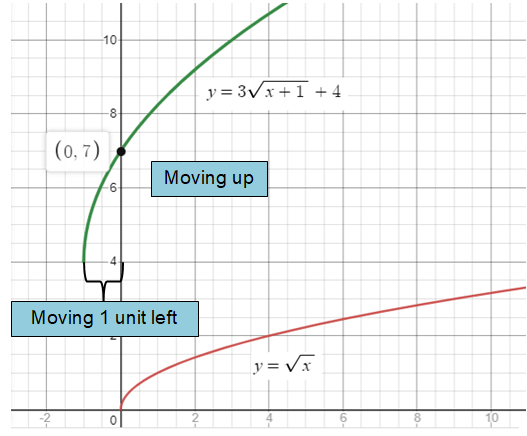
Example 5 :

Match the function with its graph. Describe the range.

a)  y = √(x - 3)       b)  y = 3√x      c)  y = √x - 3      d)  y = √(-x + 3)

Solution :

a)  y = √(x - 3)

Finding domain :

x - 3 > 0

x > 3

Domain is (3, ∞).

There is no stretch, no vertical move. So, it suits for option D.

b)  y = 3√x

Finding domain :

3√x > 0

√x > 0

Domain is (0, ∞).

There is no horizontal and vertical movement. There is vertical stretch 3 units. So, it suits for option C.

c)  y = √x - 3

Finding domain :

√x > 0

x > 0

Domain is (0, ∞).

There is no horizontal movement and vertically move 3 units down. No vertical or horizontal stretch. It suits for Option A.

d)  y = √(-x + 3)

Finding domain :

√(-x + 3)> 0

(-x + 3) > 0

-x > -3

x < 3

Domain is (-∞, -3).

y = √-(x - 3)

Refection on y-axis and moving the graph horizontally 3 units right. It suits for Option B.

Example 6 :

Match each function with its graph. Explain your reasoning.

A) f (x) = √x + 2

B. m(x) = f (x) − 4

C. n(x) = f (−x)

D. p(x) = f (3x)

Solution :

A) f (x) = √x + 2

Finding the domain :

√x > 0

x > 0

f (x) = √x + 2

By comparing the graph, y = a √(x - h) + k

There is no stretch, no horizontal movement and vertically 2 units up.

Applying x = 4, we get

f (4) = √4 + 2

= 2 + 2

f(4) = 4

So, graph B represents the function f (x) = √x + 2.

B. m(x) = f (x) − 4

Moving the graph B, 4 units down. So, graph D is correct.

C. n(x) = f (−x)

f (-x) = √-x + 2

Reflection across y-axis. So, graph C is correct.

D. p(x) = f (3x)

f (x) = √x + 2

f (3x) = √3x + 2

Vertical stretch of 3 units, graph A is correct.

Example 7 :

The graph represents the function f(x) = √x

a. What is the minimum value of the function?

b. Does the function have a maximum value? Explain.

c. Write a square root function that has a maximum value. Does the function have a minimum value? Explain

d. Write a square root function that has a minimum value of −4

Solution :

a) Minimum value of the given square root function is 0.

b) The function is increasing, there is no maximum value.

c) Since it is the square root function it is defined for the value 0, it is not defined for negative values of x. So, the minimum value is 0 and there is not maximum value.

d) Minimum value cannot be negative. So, -4 cannot be the minimum value.