GRAPHING LINES IN DIFFERENT FORMS

Graph the equation using any method.

Problem 1 :

6y = 3x + 6

Solution :

6y = 3x + 6

Divide each side by 6.

y = (3/6) x + (6/6)

y = (1/2) x + 1

The above equation is in the form y = mx + b

Then,

Slope (m) = 1/2

y-intercept = 1

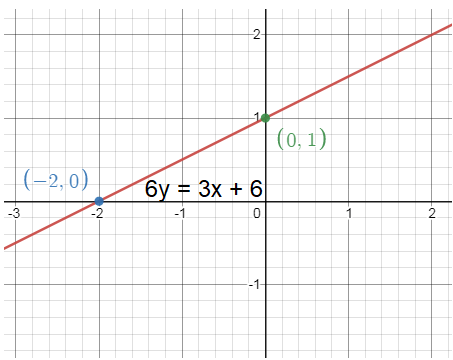
Problem 2 :

-3 + x = 0

Solution :

-3 + x = 0

x = 3

Since x = 3 is a vertical line, there is no y-intercept and the slope is undefined.

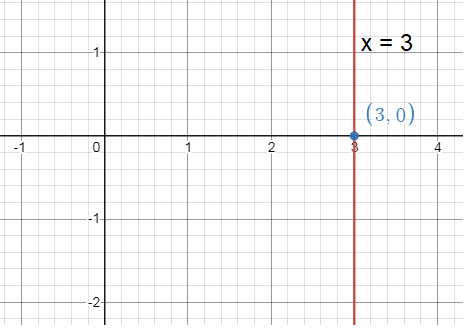
Problem 3 :

4y = 16

Solution :

y = 4

y = 0x + 4

The above equation is in the form y = mx + b

Then,

Slope (m) = 0

y-intercept = 4

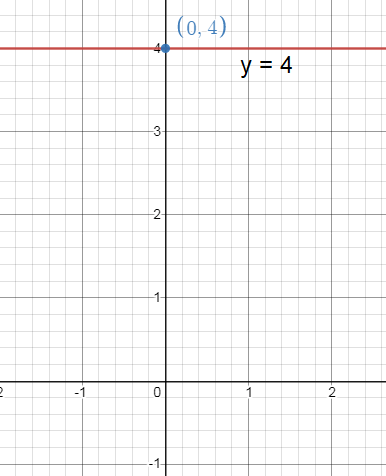
Problem 4 :

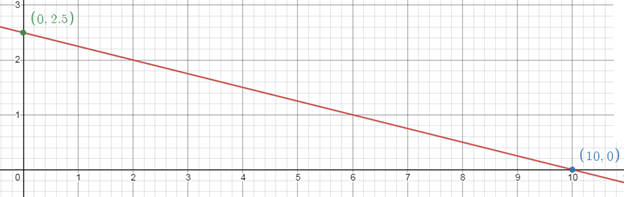
8y = -2x + 20

Solution :

To find x and y intercept we have to compare given equation with intercept form (x/a) + (y/b) = 1

2x + 8y = 20

Dividing by 20 on both sides,

(2x/20) + (8y/20) = 1

(x/10) + (2y/5) = 1

x -intercept (a) = 10

y -intercept (b) = 5/2

Problem 5 :

-4x = 8y + 12

Solution :

8y = -4x - 12

Divide each side by 8.

y = (-4/8) x - (12/8)

y = (-1/2) x - (3/2)

The above equation is in the form y = mx + b

Then,

Slope (m) = -1/2

y-intercept = -3/2

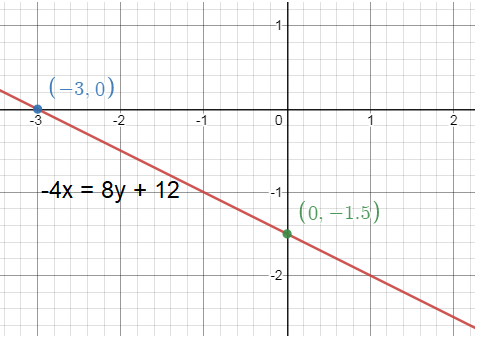
Problem 6 :

3.5x = 10.5

Solution :

3.5x = 10.5

x = 3

Since x = 3 is a vertical line, there is no y-intercept and the slope is undefined.

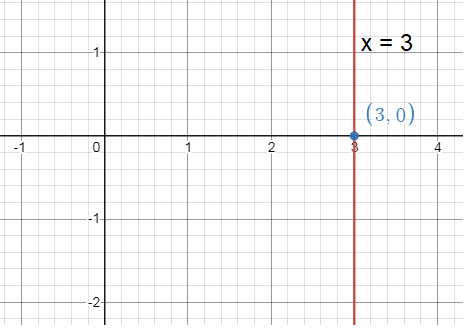
Problem 7 :

14 - 3x = 7y

Solution :

7y = -3x + 14

To find x and y intercept we have to compare given equation with intercept form (x/a) + (y/b) = 1

3x + 7y = 14

Dividing by 14 on both sides,

(3x/14) + (7y/14) = 1

(3x/14) + (y/2) = 1

x-intercept = 14/3

y-intercept = 2

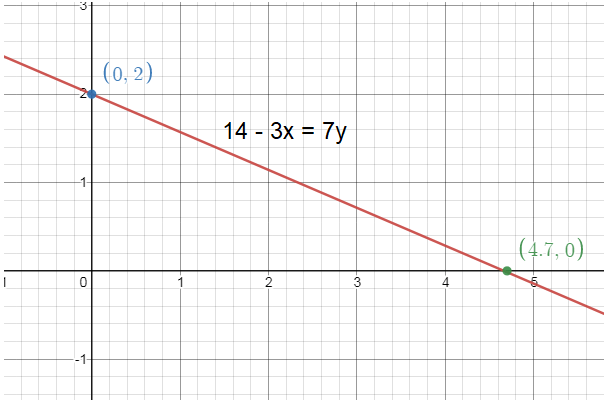
Problem 8 :

2y - 5 = 0

Solution :

2y = 0x + 5

y = 5/2

The above equation is in the form y = mx + b

Then,

Slope (m) = 0

y-intercept = 5/2

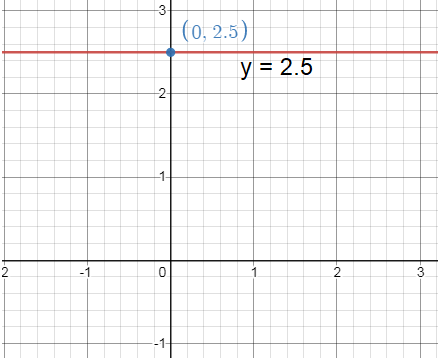
Problem 9 :

Refer to the graph.

a. Which lines have positive slopes?

b. Which line has the steepest slope?

c. Do any lines have an undefined slope? Explain.

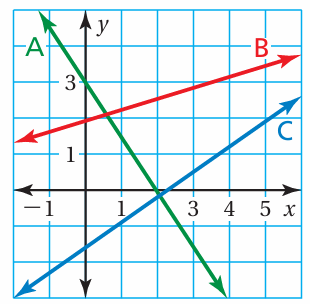
Solution :

a. While observing the lines from left to right, both B and C are raising lines. Then they will have positive slope.

b. Comparing the raisign lines, falling line has more slope and it is steepest.

c. There is no perpendicular lines. Only perpendicular line has undefined slope. So, no.

Problem 10 :

The slope of a line is 0. What do you know about the line?

Solution :

Slope = Rise / run

Here

rise = number of units moving vertically

run = number of unist moving horizontally

When the vertical movement is 0, then the slope will be negative. So, the line which has the slope 0 must be a horizontal line.

Problem 11 :

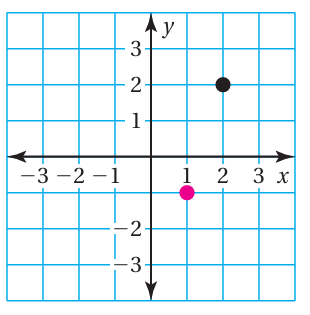
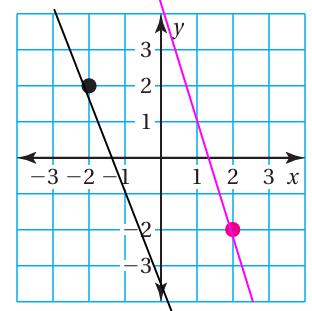
Draw a line through each point using the given slope. What do you notice about the two lines?

a)  slope = 1

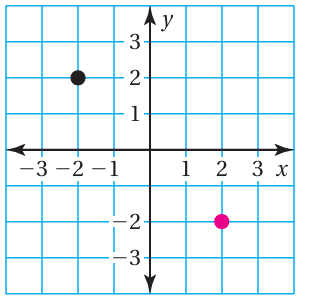
b) slope = −3

Solution :

a) In general through a point we can draw infinite number of lines. Through two points we can draw only one line. So, by tracing another point which lies on the line and having the slope 1, let us trace an another point.

Drawing the line through the line which is coloured pink :

The given slope = 1, then from that position (1, -1) move 

• vertically up of 1 unit

and

• horizontally move right of one unit.

So, another point which lies on the line will be (1 + 1, -1 + 1), that is (2, 0).

Drawing the line through the line which is coloured black :

The given slope = 1, then from that position (2, 2) move 

• vertically up of 1 unit

and

• horizontally move right of one unit.

So, another point which lies on the line will be (2+1, 2+1), that is (3, 3).

b) 

Drawing the line through the line which is coloured pink :

The given slope = -3/1, then from that position (2, -2) move 

• vertically up of 3 units

and

• horizontally move left of one unit.

So, another point which lies on the line will be (2-1, -2+3), that is (1, 1).

Drawing the line through the line which is coloured black :

The given slope = -3, then from that position (-2, 2) move 

• vertically down of 3 units

and

• horizontally move right of one unit.

So, another point which lies on the line will be (-2+1, 2-3), that is (-1, -1).

Problem 12 :

Is it more difficult to walk up the ramp or the hill? Explain.

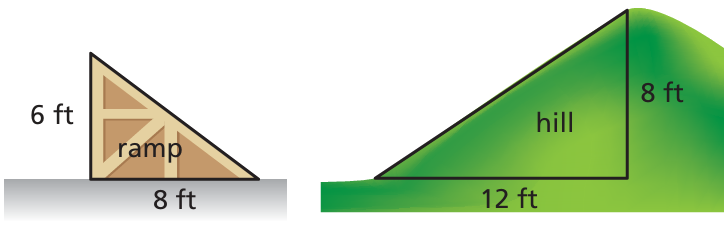
Solution :

By measuring the slope, we will get to know which one is steeper.

Slope = rise/run

Slope of ramp is greater, then it is difficult to walk in ramp.