GRADE 6 REVIEW EOG MATH

Problem 21 :

Jeff recorded the average temperatures for six months. He will display the temperatures on a number line

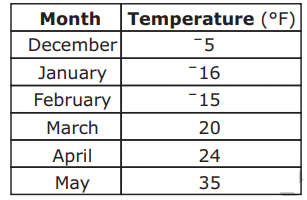
On the number line, which month’s temperature will be between February’s and March’s temperatures?

A)  December      B) January     C) April     D) May

Solution :

Temperature is February = -15

Temperature is March = 20

Difference between two temperatures = 20 - (-15)

= 20 + 15

= 35

Problem 22 :

A trapezoid in a coordinate plane has vertices 

(-2, 5) (-3, -2) (2, -2) (1, 5)

What is the height of the trapezoid?

A) 3 units     B) 5 units      C) 7 units   D) 9 units

Solution :

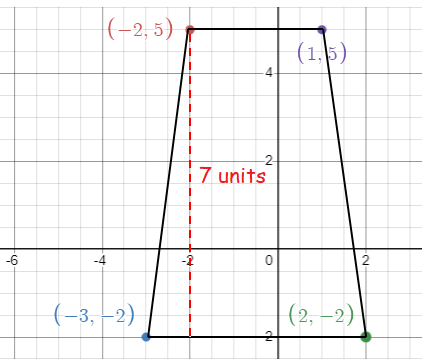
So, the answer is 7 units.

Problem 23 :

Which can be represented by the expression 17 – 2x?

A) 17 less than twice a number x

B) the difference between 17 and twice a number x

C) a number x squared, subtracted from 17

D) 17 less than a number x squared

Solution :

17 – 2x

We have negative sign, so we use the word difference.

2x = twice the number

So, difference between 17 and twice a number, option B is correct.

Problem 24 :

Which expression is equivalent to 5y + 2y + 6x + 2y – x?

A) 5x + 6y     B) 5x + 7y     C) 5x + 9y    D) 7x + 7y

Solution :

5y + 2y + 6x + 2y – x

Combining like terms, we get

= 6x - x + 2y + 2y + 5y

= 5x + 9y

So, option C is correct.

Problem 25 :

Diana can use the equation y = 7x to calculate her pay, where y represents the amount of pay, and x represents the number of hours worked. How many hours did Diana work if she was paid $45.50?

A) 5.5 hours      B) 6 hours     C) 6.5 hours     D) 7 hours

Solution :

y = 7x

y = amount of pay

x = number of hours worked

Amount of pay = 45.50

7x = 45.50

x = 45.50/7

x = 6.5

So, option C 6.5 hours is correct.

Problem 26 :

If y – 18 = 14, what is the value of 3(y + 5)?

A)  27      B) 32      C) 96      D) 111

Solution :

y – 18 = 14

y = 14 + 18 ==> 32

Applying the value of y, in 3(y + 5).

= 3(32 + 5)

= 3(37)

= 111

So, the answer is option D, 111.

Problem 27 :

Karen recorded her walking pace in the table below. What equation best represents this relationship?

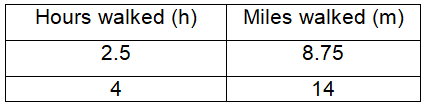
A) h = m + 10      B) h = 3.5m     C) m = h + 10   D) m = 3.5h

Solution :

h - independent variable

m - dependent variable

Rate of change :

(2.5, 8.75) and (4, 14)

Rate of change = (14 - 8.75) / (4 - 2.5)

= 5.25 / 1.5

= 3.5

Equation representing the given table :

m = 3.5h

So, option D is correct.

Problem 28 :

The shaded area indicates the parking lot at a shopping center.

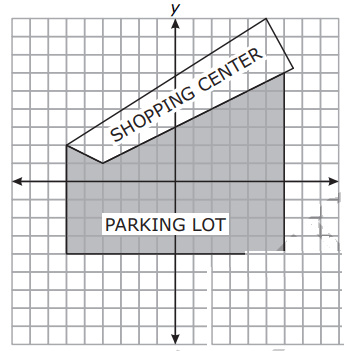
What is the total area of the parking lot?

A) 72 units²     B) 86 units²     C) 91 units²      D) 120 units²

Solution :

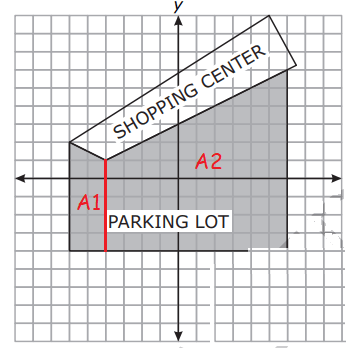
We decompose the given shaded region into two trapezium.

Area of trapezium = (1/2) h (a + b)

= 11 + 75

= 86 square units.

So, option B is correct.

Problem 29 :

The right rectangular prism below is made up of 8 cubes. Each cube has an edge length of 1/2 inch.

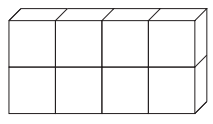
What is the volume of this prism?

A) 1 cubic inch        B) 2 cubic inches

C) 4 cubic inches    D) 8 cubic inches

Solution :

Length of each edge = 1/2 inch

length of prism = 4(1/2) = 2 inches

Width = 1/2 inch

Height = 2(1/2) ==> 1 inch

Volume = length x width x height

= 2 x (1/2) x 1

= 1 cubic inch

So, option A is correct.

Problem 30 :

What is the area of the quadrilateral with vertices at

(-1, 0), (2, 0), (2, 5) and (-1, 5)?

A) 15 square units    B) 12 square units

C) 10 square units    D) 5 square units

Solution :

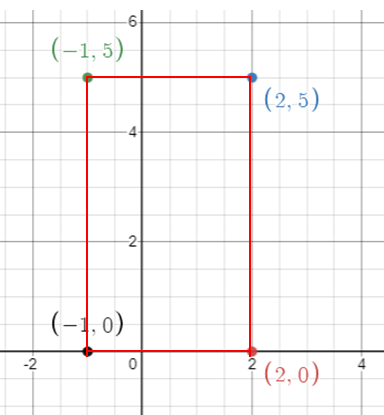
The given quadrilateral is a rectangle.

Area of rectangle = length x width

Length = 5, width = 3

= 5 x 3

= 15 square units.

So, option A is correct.