FUNCTIONS AND THEIR INVERSES MATH 3 PRACTICE PROBLEMS

Write the slope intercept form of each equation 

Problem 1 :

through (1, 3) and slope = -2/3

Solution :

Since the line is passing through the point and having given slope, we can use the formula below to find equation of the line.

y - y₁ = m(x - x₁)

(x₁, y₁) ==> (1, 3) and slope (m) = -2/3

y - y₁ = m(x - x₁)

y - 3 = (-2/3)(x - 1)

3(y - 3) = -2(x - 1)

3y - 9 = -2x + 2

2x + 3y - 9 - 2 = 0

2x + 3y - 11 = 0

Problem 2 :

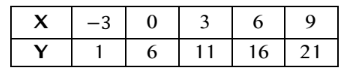
Solution :

Two points (-3, 1) and (0, 6)

Slope = (y₂ - y₁) / (x₂ - x₁)

= (6 - 1) / (0 + 3)

= 5/3

y - y₁ = m(x - x₁)

m = 5/3 and (0, 6)

y - 6 = (5/3)(x - 0)

3y - 18 = 5x

5x - 3y + 18 = 0

Use the points or graph to write a quadratics equation in the specified form. 

Problem 3 :

Write the intercept form (-4, 0) (0, 0) and (-2, 20)

Solution :

Intercept form of quadratic function will be

y = a(x - p) (x - q) ----(1)

Here p and q are x-intercepts.

y = a(x - (-4)) (x - 0)

y = a(x + 4) x

y = ax (x + 4)

Applying the point (-2, 20), we get

20 = a(-2)(-2 + 4)

20 = -2a(2)

-4a = 20

a = 20/(-4)

a = -5

Applying the value of a, we get

y = (-5)x (x + 4)

y = -5x (x + 4)

y = -5x² - 20x

Problem 4 :

Write the vertex form

 Vertex (-6, -100) and (0,44)

Solution :

Equation of quadratic function in vertex form

y = a(x - h)² + k

y = a(x - (-6))² - 100

y = a(x + 6)² - 100 -----(1)

Applying the point (0, 44), we get

44 = a(0 + 6)² - 100

44 + 100 = a(6)²

36a = 144

a = 144/36

a = 4

By applying the value of a in (1), we get

y = 4(x + 6)² - 100

Problem 5 :

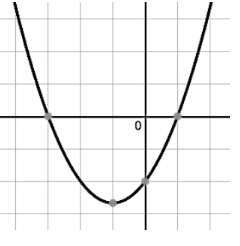
Solution :

From the graph show above, it is clear that the x-intercepts are -3 and 1.

y-intercept is -2.

y = a(x - p)(x - q)

Here p and q are x-intercepts.

y = a(x - (-3))(x - (-1))

y = a(x + 3)(x + 1) -------(1)

Since the y-intercept is -2, by applying (0, -2)

-2 = a(0 + 3)(0 + 1)

-2 = a(3)

a = -2/3

Applying the value of a in (1), we get

y = (-2/3) (x + 3)(x + 1)

y = (-2/3) (x² + 3x + 1x + 3)

y = (-2/3) (x² + 4x + 3)

y = (-2/3) (x² + 4x + 3)

Convert each function into intercept form.

Problem 6 :

m(x) = -x² - 5x + 36

Solution :

m(x) = -x² - 5x + 36

Factoring 36, we get -9 and 4

m(x) = -x² - 9x + 4x + 36

= -x(x + 9) + 4(x + 9)

= (-x + 4)(x + 9)

So, the intercept form is (-x + 4)(x + 9).

Problem 7 :

y = (x - 1)² - 4

Solution :

y = (x - 1)² - 4

y = x² - 2x + 1 - 4

y = x² - 2x - 3

Factoring -3, we get -3 and 1

y = x² - 3x + 1x - 3

= x(x - 3) + 1(x - 3)

y = (x + 1)(x - 3)

Problem 8 :

y = 5x² - 30x - 80

Solution :

y = 5x² - 30x - 80

Factoring 5, we get

y = 5(x² - 6x - 16)

y = 5(x² - 8x + 2x - 16)

y = 5[x(x - 8) + 2(x - 8)]

y = 5(x + 2)(x - 8)

Convert each function in vertex form :

Problem 9 :

y = x² + 10x - 56

Solution :

y = x² + 10x - 56

To convert into vertex form, we get

y + 56 = x² + 10x

y + 56 = x² + 2 x (5) + 5² - 5²

y + 56 = (x + 5)² - 25

y = (x + 5)² - 25 - 56

y = (x + 5)² - 81

Problem 10 :

y = x² + 4x - 12

Solution :

y = x² + 4x - 12

To convert into vertex form, we get

y + 12 = x² + 4x

y + 12 = x² + 2 x (2) + 2² - 2²

y + 12 = (x + 2)² - 2²

y = (x + 2)² - 4 - 12

y = (x + 2)² - 16

Problem 11 :

y = 4(x - 6)(x + 4)

Solution :

y = 4(x - 6)(x + 4)

To convert into vertex form, we get

y = 4(x² + 4x - 6x - 24)

y = 4(x² - 2x - 24)

y = 4(x² - 2x(1) + 1² - 1² - 24)

y = 4[(x - 1)² - 1 - 24]

y = 4[(x - 1)² - 25]

y = 4(x - 1)² - 100

List the important features of each quadratic 

a) x--intercepts    b)  vertex     c) Axis of symmetry

d) y-intercept      e) opens      f)  max/min

g)  Domain      h) Range

Problem 12 :

f(x) = (1/2)(x - 3)(x + 5)

Solution :

a) x--intercepts :

f(x) = (1/2)(x - 3)(x + 5)

Since the quadratic function is in intercept form, we can compare the given function f(x) with y = a(x - p)(x - q). Where p and q are x-intercepts.

For the given function f(x) 3 and -5 are x-intercepts.

b)  vertex :

f(x) = (1/2)(x² + 5x - 3x - 15)

= (1/2)(x² + 2x - 15)

= (1/2)(x² + 2x(1) + 1² - 1² - 15)

= (1/2)[(x + 1)² - 1 - 15]

= (1/2)[(x + 1)² - 16]

= (1/2)(x + 1)² - 8

Comparing with y = a(x - h)² + k

Here vertex is (h, k) ==> (-1, 8).

c) Axis of symmetryc :

To find axis of symmetry, we use the formula x = -b/2a or x = h

x = -1

d) y-intercept :

To find y-intercept, we put x = 0

f(0) = (1/2)(0 - 3)(0 + 5)

f(0) = -15/2 ==> -7.5

e) opens :

Since the coefficient of x² is positive, it opens up.

f)  max/min :

Since it opens up, it will have minimum value and at (-1, 8).

g)  Domain :

All real values, (-∞, ∞)

h) Range :

y ≥ -8, (-8, ∞)