FUNCTION NOTATIONS ON SAT

Problem 1 :

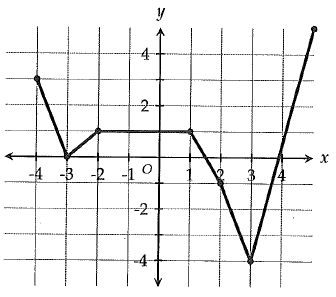
The graph above shows the function g. What is value of g(3) ?

a)  -4      b)   0     c) 3       d)  4

Solution :

By drawing the vertical line at x = 3, the curve will cross the vertical line at -4. So, the value of g(3) is -4.

Problem 2 :

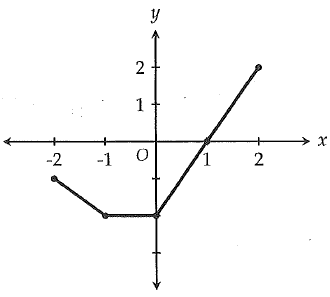
The graph of f(x) is shown in the xy plane above. If f(a) = -2, which of the following is a possible value of a.

a)  -1.5      b)   -0.5    c) 1       d)  2

Solution :

f(a) = -2

By observing the graph, on the x-axis for all values between -1 to 0, we have -2. From the given options -0.5 will be correct.

Problem 3 :

The function f is defined by f(x) = (1/2)x + a, where a is constant. If f(a) = 3, what is the value of f(8) ?

Solution :

Given function is 

f(x) = (1/2)x + a  ----(1)

f(a) = 3

When x = a, y = 3

f(a) = (1/2)a + a

3 = a/2 + a

3 = 3a/2

6 = 3a

a = 6/3

a = 2

By applying the value of a in (1), we get

f(x) = (1/2)x + 2

f(8) = (1/2)8 + 2

f(8) = 4 + 2

f(8) = 6

Problem 4 :

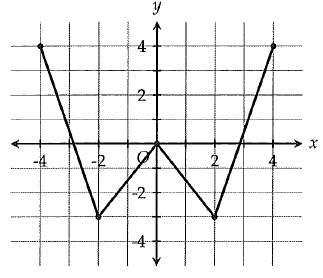
The complete solution f is shown in the xy plane. If f(x) = k has two solutions, which of the following could be the value of k ?

I)  -3       II) 0      III)  2.5

a)  I and II     b)  III only     c)  I and III only     d)  I, II and III

Solution :

Consider f(x) = k

By observing the graph, by drawing horizontal line y = -3, the curve will intersect the horizontal line, we get two different solutions -2 and 2.

Drawing the line y = 0,  we get three solutions

Drawing the line y = 2.5, we get two different solutions.

So, option c will be correct.

Problem 5 :

p(t) = -t² + 16t + k

The price of a stock on day number t can be modeled by the function p above, where k is a constant and 1 ≤ t ≤ 15. On what number day was the price of the stock equal to what it was on day number 3 ?

a)    9       b)  11       c)  13      d)   15

Solution :

p(t) = p(3)

-t² + 16t + k = -(3)² + 16(3) + k

-t² + 16t + k = -9 + 48 + k

-t² + 16t = 39

-t² + 16t - 39 = 0

t² - 16t + 39 = 0

(t - 13)(t - 3) = 0

t = 13 and t = 3

So, on the day number 13 the price will also be equal.

Problem 6 :

The function y = f(x), defined for -3 ≤ x ≤ 4 is graphed in the xy plane above. Which of the following gives all values of x for which f(x) is negative ?

a)  -3 ≤ x ≤ 4      b)  -2 < x ≤ 4

c)  -2 < x < 0 and 3 < x ≤ 4

d)  -3 ≤ x < -2 and 0 < x < 3

Solution :

By observing the graph, after -2 up 0, for all values of x, we will get negative values.

After 3, for all values of x, we will receive negative values as result.

So, the answer is c)  -2 < x < 0 and 3 < x ≤ 4.

Problem 7 :

The functions f and g are defined by

f(x) = x² + 2 and g(x) = 4x - 3.

If a > 0, for what value of a does g(f(a)) = 41 ?

Solution :

f(x) = x² + 2 and g(x) = 4x - 3.

f(a) = a² + 2

g(f(a)) = g(a² + 2)

41 = 4(a² + 2) - 3

41 = 4a² + 8 - 3

41 = 4a² + 5

41 - 5 = 4a²

36 = 4a²

a² = 36/4

a² = 9

a = 3 and -3

Since a > 0, the answer is 3.

Problem 8 :

v = 550 - 9.8t

The equation above gives the velocity v of a ball t seconds after it is thrown vertically upwards with an initial velocity of 550 meters per second. After approximately how many seconds will the ball stop and start drop back to the ground ?

a)  47.8    b)  51.4       c)  55.5     d)  56.1

Solution :

At the maximum height, the velocity will be 0.

0 = 550 - 9.8t

9.8t = 550

t = 550/9.8

t = 56.122

So, option d is correct.

Problem 9 :

If f(x + 1) = 3x + 2, the function f could be defined by which of the following ?

a)  f(x) = 3x - 2      b)  f(x) = 3x - 1

c)  f(x) = 3x + 1      d)  f(x) = 3x + 5

Solution :

So, the function f(x) is 3x - 1.

Problem 10 :

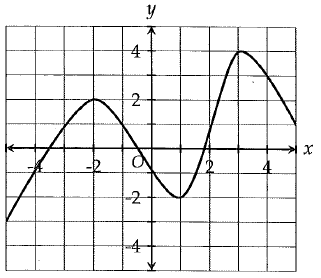
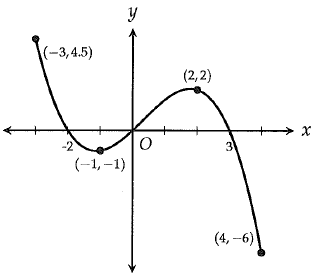
What is the difference between the minimum and maximum values of the function graphed in the xy plane for -5 ≤ x ≤ 5 ?

Solution :

The maximum point is at (3, 4) and minimum point is at (1, -2).

Maximum value = 4, minimum value = -2

Difference between maximum and minimum value = 4 - (-2)

= 4 + 2

= 6

So, the answer is 6.

Problem 11 :

A function f(x) has two properties

f(a + b) = f(a) - b

f(2) = 10

What is the  value of f(5) ?

a)  5     b)  7     c)  9       d)  11

Solution :

f(5) = f(2 + 3)

f(2 + 3) looks like f(a + b),

f(a + b) = f(a) - b

f(2 + 3) = f(2) - 3

= 10 - 3

= 7

So, option b is correct.

Problem 12 :

f(x) = x + 2, if x ≥ 0

f(x) = x - 2, if x < 0

The function f is defined above. Which of the following cannot be f(x) for any value of x ?

a)  -6      b)  -4     c)  1    d) 3

Solution :

When x = -4, f(-4) = -6 (option a is possible)

When x = -2, f(-2) = -4 (option b is possible)

When x = 1, f(1) = 3 (option d is possible)

We will receive 1 only when x = 3 (from x + 2). If we want to receive 1 from the second function, we should apply 3 instead of x. That is not possible. So 1 cannot be the value of f(x). 

Problem 13 :

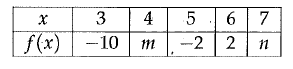
The values in the table above define a linear function. What is the value of m + n ?

a)  -4     b) 0     c)  4        d)  8

Solution :

Let the linear function be y = ax + b

When x = 3, y = -10

-10 = 3a + b-------(1)

When x = 5, y = -2

-2 = 5a + b-------(2)

(1) - (2)

3a - 5a + b - b = - 10 + 2

-2a = -8

a = 4

Applying the value of a in (1), we get

-10 = 3(4) + b

-10 = 12 + b 

b = -22

y = 4x - 22

m + n = -6 + 6 ==> 0

So, the value of m + n is 0.