FROM THE TABLE OF VALUES FOR FUNCTIONS EVALUATE THE COMPOSITE FUNCTION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
To find composition of functions from the table of values given, let us look at the example.
(f ∘ g)(x) = f [g(x)]
- x is the input. From the table, find the output for the function g.
- Let g(x) = a
- Now the original function will become f [a].
- Now a is the input. From the table, find the output for the function f.
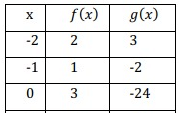
(f ∘ g)(-1) = f [g(-1)]
When -1 is the input, calculating the value of the function g, we get
(f ∘ g)(-1) = f [-2]
When the input is -2, the value of the function f, we get
(f ∘ g)(-1) = 2
Using a table to find the value of a composite function.
Problem 1 :
Use the table to find the indicated function values.
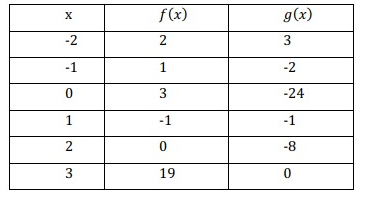
|
1. f(g(3)) 2. f(g(1)) 3. g(f(-2)) 4. g(f(-1)) |
5. g(f(0)) 6. g(g(-2)) 7. f(f(0)) 8. g(f(1)) |
Solution:
1.
f(g(3))
When 3 is the input, calculating the value of the function g, we get
f(g(3)) = f [0]
When the input is 0, the value of the function f, we get
f(g(3)) = 3
2.
f(g(1))
When 1 is the input, calculating the value of the function g, we get
f(g(1)) = f [-1]
When the input is -1, the value of the function f, we get
f(g(1)) = 1
3.
g(f(-2))
When -2 is the input, calculating the value of the function f, we get
g(f(-2)) = g[2]
When the input is 2, the value of the function g, we get
g(f(-2)) = -8
4.
g(f(-1))
When -1 is the input, calculating the value of the function f, we get
g(f(-1)) = g[1]
When the input is 1, the value of the function g, we get
= -1
5.
g(f(0))
When 0 is the input, calculating the value of the function f, we get
g(f(0)) = g[3]
When the input is 3, the value of the function g, we get
g(f(0)) = 0
6.
g(g(-2))
When -2 is the input, calculating the value of the function g, we get
g(g(-2)) = g[3]
When the input is 3, the value of the function g, we get
= 0
7.
f(f(0))
When 0 is the input, calculating the value of the function f, we get
f(f(0)) = f[3]
When the input is 3, the value of the function f, we get
= 19
8.
g(f(1))
When 1 is the input, calculating the value of the function f, we get
g(f(1)) = g[-1]
When the input is -1, the value of the function g, we get
= -2
Problem 2 :
The functions f(x) and g(x) are defined by the tables below.
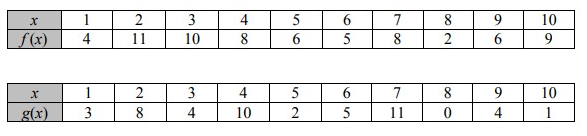
1.f(g(5)) =
2. f(g(1)) =
3. g(f(4)) =
4. f(f(1)) =
Solution:
1.
f(g(5))
When 5 is the input, calculating the value of the function g, we get
f(g(5)) = f[2]
When the input is 2, the value of the function f, we get
= 11
2.
f(g(1))
When 1 is the input, calculating the value of the function g, we get
f(g(1)) = f[3]
When the input is 3, the value of the function f, we get
= 10
3.
g(f(4))
When 4 is the input, calculating the value of the function f, we get
g(f(4)) = g[8]
When the input is 8, the value of the function g, we get
= 0
4.
f(f(1))
When 1 is the input, calculating the value of the function f, we get
f(f(1)) = f[4]
When the input is 4, the value of the function f, we get
= 8
Problem 3 :
Use the tables of the functions f and g.
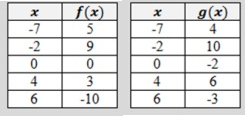
1. (f ∘ g)(-7)
2. f(g(0))
3. (f ∘ g)(4)
Solution:
1.
(f ∘ g)(-7) = f(g(-7))
When -7 is the input, calculating the value of the function g, we get
f(g(-7)) = f[4]
When the input is 4, the value of the function f, we get
(f ∘ g)(-7) = 3
2.
f(g(0))
When 0 is the input, calculating the value of the function g, we get
f(g(0)) = f[-2]
When the input is -2, the value of the function f, we get
= 9
3.
(f ∘ g)(4) = f(g(4))
When 4 is the input, calculating the value of the function g, we get
f(g(4)) = f[6]
When the input is 6, the value of the function f, we get
(f ∘ g)(4) = -10
Problem 4 :
The functions A(x) and B(x) are defined by the tables below.
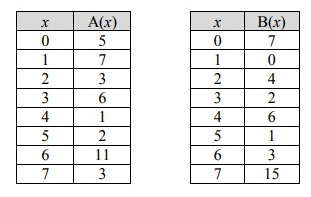
a) A(B(4)) = ___
b) B(A(1)) = ___
c) B(A(7)) = ___
d) A(B(1)) = ___
Solution:
a)
A(B(4))
When 4 is the input, calculating the value of the function B, we get
A(B(4)) = A[6]
When the input is 6, the value of the function A, we get
= 11
b)
B(A(1))
When 1 is the input, calculating the value of the function A, we get
B(A(1)) = B[7]
When the input is 7, the value of the function B, we get
= 15
c)
B(A(7))
When 7 is the input, calculating the value of the function A, we get
B(A(7)) = B[3]
When the input is 3, the value of the function B, we get
= 2
d)
A(B(1))
When 1 is the input, calculating the value of the function B, we get
A(B(1)) = A[0]
When the input is 0, the value of the function A, we get
= 5
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling