FROM THE TABLE OF VALUES CHECK IF IT IS LINEAR OR QUADRATIC

Problem 1 :

The table shows the heights y of a competitive water-skier x seconds jumping off a ramp. Write a function that models the height of the water-skier over time. When is the water-skier 5 feet above the water? How long is the skier in the air?

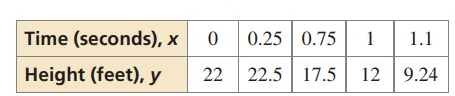
Solution:

y = ax² + bx + c

By applying point (x, y) = (0, 22)

22 = a(0) + b(0) + c

c = 22

y = ax² + bx + 22

For x = 1, y = 12,

12 = a + b + 22

a + b = -10 ---> (1)

For x = 1/4, y = 22.5

22.5 = (1/16)a + (1/4)b + 22

1/16a + 1/4b = 0.5 ---> (2)

Substitute a = -16 in (1)

a + b = -10

-16 + b = -10

b = 6

y = -16x² + 6x + 22 

When water skier 5 feet above water,

Put y = 5

5 = -16x² + 6x + 22

-16x² + 6x + 17 = 0

a = -16, b = 6 and c = 17

Time = 1.235 seconds

analyze the differences in the outputs to determine whether the data are linear, quadratic, or neither. Explain. If linear or quadratic, write an equation that fits the data.

Problem 2 :

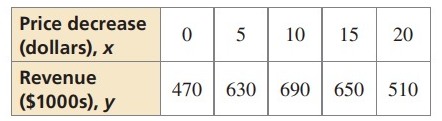
Solution :

Since the second difference is the same, it is a quadratic equation.

y = ax² + bx + c

By applying point (x, y) = (0, 470)

470 = a(0) + b(0) + c

c = 470

y = ax² + bx + 470

For x = 5, y = 630

630 = 25a + 5b + 470

25a + 5b = 160 ---> (1)

For x = 10, y = 690

690 = 100a + 10b + 470

100a + 10b = 220 ---> (2)

(1) × 2 - (2) ==> (50a + 10b) - 100a + 10b = 320 - 220

-50a = 100

a = -2

By applying a = -2 in (1)

25(-2) + 5b = 160

-50 + 5b = 160

5b = 210

b = 42

So, the required function that models the given table is 

y = -2x² + 42x + 470

Problem 3 :

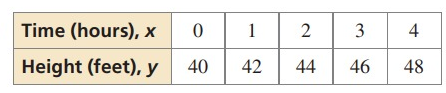
Solution :

Since the first difference is the same, it must be a linear function.

y = mx + c

For x = 0, y = 40

40 = m(0) + c

c = 40

For x = 1, y = 42

42 = m(1) + 40

42 = m + 40

m = 2

So, the required equation which models the table is 

y = 2x + 40

Problem 4 :

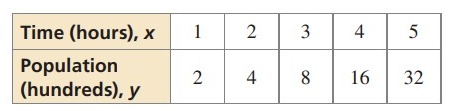
Solution:

Any of the 1^st, 2^nd, 3^rd difference are not same. Then it is not a linear function.

Problem 5 :

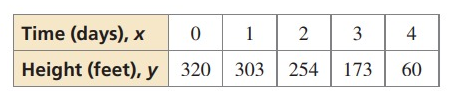
Solution :

Since the third difference is the same, it must be a cubic polynomial.