FROM THE GIVEN INFORMATION FIND EQUATION OF PARABOLA

Write an equation in standard form for the parabola satisfying the given conditions.

Problem 1 :

Focus: (9, 0); Directrix: x = -9

Solution:

From the given information, we know that the given parabola is symmetric about x-axis and it is open rightward.

Equation of the parabola with vertex (0, 0)

y² = 4ax

Here a = 9

y² = 4(9)x

y² = 36x

Problem 2 :

Focus: (-10, 0); Directrix: x = 10

Solution:

From the given information, we know that the given parabola is symmetric about x-axis and it is open leftward.

Equation of the parabola with vertex (0, 0)

y² = -4ax

Here a = 10

y² = -4(10)x

y²= -40x

Problem 3 :

Vertex: (5, -2); Focus (7, -2)

Solution:

The parabola is symmetric about x-axis and open right ward.

(y - k)² = 4a(x - h)

Here (h, k) = (5, -2) and F(7, -2)

Distance between vertex and focus = a

a = √(5 - 7)² + (-2 + 2)²

a = √(-2)²

a = √4

a = 2

(y + 2)² = 4(2)(x - 5)

(y + 2)² = 8(x - 5)

Problem 4 :

Focus: (2, 4); Directrix: x = -4

Solution:

Let (h, k) be the vertex of parabola. 

(y - k)² = 4a(x - h)

Vertex and focus must lie on the axis and hence they share same y-coordinate

k = 4

Vertex lies midpoint between directrix and focus

Vertex (h, k) = (-1, 4)

h + a = 2

-1 + a = 2

a = 3

(y - 4)² = 4(3)(x + 1)

(y - 4)² = 12(x + 1)

Problem 5 :

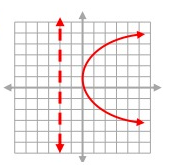
Solution:

From a given graph,

Vertex (h, k) = (0, 1)

Directrix: x = -2

(y - k)² = 4a(x - h)

The parabola that opens to the right with a focus at a distance a = 2

(y - 1)² = 4(2)(x - 0)

(y - 1)² = 8x

Problem 6 :

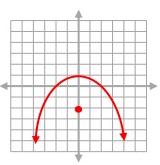
Solution:

From a given graph,

Vertex (h, k) = (0, 1)

Focus = (0, -2)

 (x - h)² = -4a(y - k)

Distance between vertex and focus = a

a = √(0 - 0)² + (1 + 2)²

a = √3²

a = √9

a = 3

(x - 0)² = -4(3)(y - 1)

x² = -12(y - 1)