FROM MINIMUM AND MAXIMUM POINT FIND EQUATION OF SINUSOIDAL FUNCTION

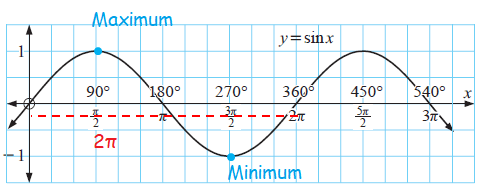
Amplitude Period Maximum and Minimum of Sine Functions

A periodic function is one which repeats itself over and over in horizontal direction.

What is period ?

The period of a periodic function is the length of one repetition or cycle

What is amplitude ?

The amplitude is the vertical distance between a maximum point and the principal axis.

What is maximum and minimum ?

• The maximum points occurs at the top of the crest.
• The minimum points occurs at the bottom of a through.

What is principal axis or man line ?

The graph oscillates about horizontal line called the principal axis or mean line.

y = A sin (B(x - h)) + k

or

y = A cos (B(x - h)) + k

Amplitude = (y coordinate of max - y coordinate of min)/2

Vertical shift = (y coordinate of max + y coordinate of min)/2

Period = 2|x coordinate of max - x coordinate of min|

Frequency = 2π/T

Where T is the period 

Phase shift for sin :

x-coordinate of max

Phase shift for cos :

x coordinate of max - T/4

• The amplitude is |A|
• Period is 2π/|k|, for B > 0

Problem 1 :

The trigonometric function k has a maximum at the point (0, 8). After this maximum , the next minimum occurs at the point (2π, 2). Which of the following could be the expression for k(x) ?

a) 3 cos (x/2) + 5     b) 3 cos (2x) + 5      c) 3 sin (x/2) + 5    d) 3 sin (2x) + 5

Solution :

x-coordinate of maximum = 0

y-coordinate of maximum = 8

x-coordinate of minimum = 2π

y-coordinate of minimum = 2

Amplitude = (y coordinate of max - y coordinate of min)/2

= (8 - 2)/2

= 3

Vertical shift = (y coordinate of max + y coordinate of min)/2

= (8 + 2)/2

= 5

Period = 2|x coordinate of max - x coordinate of min|

= 2|0 - 2π|

= 2|2π|

= 4π

Frequency = 2π/T

Where T is the period 

= 2π/4π

= 1/2

It must be the cosine function, because the cos (0) = 1

y = A cos (B(x - h)) + k

y = 3 cos (1/2(x - 0)) + 5

y = 3 cos (x/2) + 5

Problem 2 :

The trigonometric function k has a maximum at the point (π/2, 30). After this maximum , the next minimum occurs at the point (3π/2, 20). Which of the following could be the expression for k(x) ?

a) 5 cos (x) + 25     b) 10 cos x + 20      c) 5 sin x + 25    d) 10 sin x + 20

Solution :

From the given information, it is clear that the function is sin, because sin π/2 = 1

x-coordinate of maximum = π/2

y-coordinate of maximum = 30

x-coordinate of minimum = π/2

y-coordinate of minimum = 20

Amplitude = (30 - 20)/2

= 10/2

= 5

Vertical shift = (30 + 20)/2

= 50/2

= 25

Period = 2|π/2 - 3π/2|

= 2|-2π/2|

= 2π

Frequency = 2π/2π

= 1

y = A sin (B(x - h)) + k

y = 5 sin (1(x - 0)) + 25

y = 5 sin x + 25

Option c is correct.

Problem 3 :

The trigonometric function k has a minimum at (0, -6). After this minimum, the next maximum occurs at the point (3π, 0). Which of the following could be the expression for k(x) ?

a) 3 cos (3x) - 3     b) -3 cos (3x) - 3      c) 3 cos (x/3) - 3   d) -3 cos (x/3) - 3

Solution :

From the given information, it is clear that the function is cos, because cos 0  = 1 and there must be reflection, because it is not (0, 6) it is (0, -6).

x-coordinate of maximum = 3π

y-coordinate of maximum = 0

x-coordinate of minimum = 0

y-coordinate of minimum = -6

Amplitude = (0 - (-6))/2

= 6/2

= 3

Vertical shift = (0 - 6)/2

= -3

Period = 2|3π - 0|

= 6π

Frequency = 2π/T

= 2π/6π

= 1/3

y = A cos (B(x - h)) + k

y = 3 cos (1/3(x - 0)) + (-3)

y = 3 cos (x/3) - 3

Since there must be the reflection, we use negative sign

y = -3 cos (x/3) - 3

Option d is correct.

Problem 4 :

The graph of a sinusoidal function has been horizontally compressed and horizontally translated to the left. It has maximums at the points (-5π/7, 1) (-3π/7, 1) and its minimum at (-4π/7, -1). If the x-axis is in radians, what is the period of the function.

Solution :

x-coordinate of maximum = -5π/7

y-coordinate of maximum = 1

x-coordinate of minimum = -4π/7

y-coordinate of minimum = -1

Period = 2|x coordinate of max - x coordinate of minimum|

= 2 |-5π/7 - (-4π/7)|

= 2|-π/7|

= 2π/7

Problem 5 :

The graph of a sinusoidal function has been vertically stretched, vertically translated up, and horizontally translated to the right. The graph has a maximum at (π/13, 13) and the equation of axis is y = 9. If the x-axis is in radians, list one point where the graph has a minimum.

Solution :

Amplitude = 13 - 9

= 4

When maximum has its y-coordinate as 13 (going up for 4 units), its minimum will have the y-coordinate as 9 - 4 that is 5.

There is no horizontal stretch, then sinusoidal function will have the period 2π, after the maximum or minimum the next turning point will appear at 2π/2, that is in the interval of π.

π/13 + π = 14 π/13

So, the required point is (14π/13, 5).