FORMULA FOR A SQUARE MINUS B SQUARE

Expand 

Problem 1 :

x² - 16

Solution :

= x² - 16

= x² - 4²

Here a = x, b = 4

a² - b² = (a + b) (a - b)

x² - 4² = (x + 4) (x - 4)

Problem 2 :

y² - 49

Solution :

= y² - 49

= y² - 7²

Here a = y, b = 7

y² - 7² = (y + 7) (y - 7)

Problem 3 :

x² - 25

Solution :

= x² - 25

= x² - 5²

Here a = x, b = 5

x² - 5² = (x + 5) (x - 5)

Problem 4 :

4x² - 25

Solution :

= 4x² - 25

= 2²x² - 5²

= (2x)² - 5²

Here a = 2x and b = 5

(2x)² - 5² = (2x + 5) (2x - 5)

Problem 5 :

16 - y²

Solution :

(16 - y²) can be written as 4² - y²

Here a = 4 and b = y

4² - y² = (4 + y) (4 - y)

Problem 6 :

m² - 36

Solution:

= m² - 36

= m² - 6²

Here a = m, b = 6

m² - 6² = (m + 6) (m - 6)

Problem 7 :

4m² - 49

Solution :

(4m² - 49) can be written as (2m)² - 7²

Here a = 2m and b = 7

(2m)² - 7² = (2m + 7) (2m - 7)

Problem 8 :

9m² - 16

Solution:

(4m² - 49) can be written as (3m)² - 4²

Here a = 3m and b = 4

(3m)² - 4² = (3m + 4) (3m - 4)

Problem 9 :

Find the product using suitable identity :

(a + 3)(a - 3)(a² + 9)

Solution:

= (a + 3)(a - 3)(a² + 9)

= (a² - 3²)(a² + 9)

= (a² - 9)(a² + 9)

= (a²)² - 9²

= a⁴ - 81

Evaluate the following :

Problem 9 :

Find the product using suitable identity :

a) 100² - 98²

b) 73² - 67²

c) 145² - 140²

d) 651² - 641²

Solution:

a) 100² - 98²

= (100 + 98)(100 - 98)

= 198 (2)

= 396

b) 73² - 67²

= (73 + 67)(73 - 67)

= 140 (6)

= 840

c) 145² - 140²

= (145 + 140)(145 - 140)

= 285 (5)

= 1425

d) 651² - 641²

= (651 + 641)(651 - 641)

= 1292 (10)

= 12920

Find the missing sides of the following.

Problem 10 :

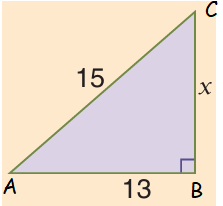
Solution :

Using Pythagorean theorem,

AC² = AB² + BC²

15² = 13² + x²

x² = 15² - 13²

x² = (15 + 13) (15 - 13)

x² = 28 (2)

x = √28 x 2

= √2 x 2 x 7 x 2

= 2 √(2 x 7)

= 2 √14

Problem 11 :

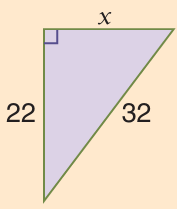
Solution :

Using Pythagorean theorem,

32² = 22² + x²

x² = 32² - 22²

x² = (32 + 22) (32 - 22)

x² = 54 (10)

x = √54 x 10

= √3 x 3 x 3 x 2 x 2 x 5

= 3 x 2 √(3 x 5)

= 6 √15

Problem 12 :

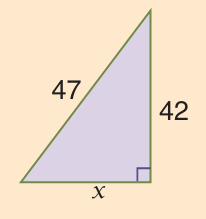
Solution :

Using Pythagorean theorem,

47² = x² + 42²

x² = 47² - 42²

x² = (47 + 42) (47 - 42)

x² = 89 (5)

x = √(89 x 5)

= √445

Problem 13 :

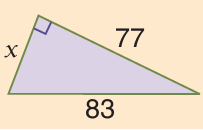
Solution :

Using Pythagorean theorem,

83² = x² + 77²

x² = 83² - 77²

x² = (83 + 77) (83 - 77)

x² = 160 (6)

x = √(160 x 6)

= √4 x 4 x 2 x 5 x 2 x 3

= (4 x 2) √(5 x 3)

= 8 √15

Problem 14 :

Simplify (y + 7)(y − 7) − (y + 7)

Solution :

= (y + 7)(y − 7) − (y + 7)

= y² - 7² - (y + 7)

= y² - 49 - y - 7

= y² - y - 49 - 7

= y² - y - 56

Problem 15 :

Simplify (x + y)² − (x − y)(x + y)

Solution :

= (x + y)² − (x − y)(x + y)

= x² + 2xy + y² - (x² - y²)

= x² + 2xy + y² - x² + y²

= 2xy + 2y²

= 2y(x + y)

Problem 16 :

(2x + 3y)² − (2x − 3y)(2x + 3y)

Solution :

= (2x + 3y)² − (2x − 3y)(2x + 3y)

= (2x)² + 2(2x)(3y) + (3y)² - [(2x)² - (3y)²]

= 4x² + 12xy + 9y² - [4x² - 9y²]

= 4x² + 12xy + 9y² - 4x² + 9y²

= 12xy + 18y²

Problem 17 :

(a − 1)(a + 1) + (a + 1)² + (a − 1)²

Solution :

= (a − 1)(a + 1) + (a + 1)² + (a − 1)²

= a² - 1² + a² + 2a + 1² + a² - 2a + 1²

= 3a² - 1 + 2a + 1 - 2a + 1

= 3a² + 1