FORMULA FOR A MINUS B THE WHOLE SQUARE

Expand and simplify :

Problem 1 :

(x - 3)²

Solution :

By comparing (a - b)² and (x - 3)² , we get

a = x, b = 3

(a - b)² = a² - 2ab + b²

Substitute x for a and 3 for b

(x - 3)² = x² - 2(x)(3) + 3²

(x - 3)² = x² - 6x + 9

Problem 2 :

(2 - x)²

Solution :

By comparing (a - b)² and (2 - x)² , we get

a = 2, b = x

(2 - x)² = 2² - 2(2)(x) + x²

(2 - x)² = 4 - 4x + x²

Problem 3 :

(3x - 1)²

Solution :

By comparing (a - b)² and (3x - 1)² , we get

a = 3x, b = 1

(3x - 1)² = (3x)² - 2(3x)(1) + (1)²

(3x - 1)² = 9x² - 6x + 1

Problem 4 :

(x - y)²

Solution :

By comparing (a - b)² and (x - y)² , we get

a = x, b = y

(x - y)² = x² - 2(x)(y) + y²

(x - y)² = x² - 2xy + y²

So, the expansion of (x - y)² is

x² - 2xy + y²

Problem 5 :

(2x – 5y)²

Solution :

Here a = 2x, b = 5y

(2x - 5y)² = (2x)² - 2(2x)(5y) + (5y)²

(2x - 5y)² = 4x² - 20xy + 25y²

So, the expansion of (2x - 5y)² is

4x² - 20xy + 25y²

Problem 6 :

(ab - 2)²

Solution:

Here a = ab, b = 2

(ab - 2)² = (ab)² - 2(ab)(2) + (2)²

(ab - 2)² = ab² - 4ab + 4

Problem 7 :

Evaluate (48)²

Solution :

(48)² = (50 - 2)²

= (50)² - 2(50)(2) + (2)²

= 2500 – 200 + 4

     = 2304

Problem 8 :

(2x/3 – 3y/2)²

Solution :

Here a = 2x/3, b = 3y/2

(2/3 x – 3/2 y)² = (2x/3)² - 2(2x/3)(3y/2) + (3y/2)²

= 4/9 x² - 2xy + 9/4 y²

Problem 9 :

By using the suitable identity, evaluate x² + 1/x², if x - 1/x = 5

Solution :

Problem 10 :

Find the length of the side of the given square if area of the square is 625 square units and then find the value of x.

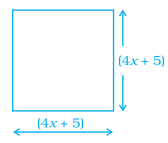
Solution :

Area of the square = 625

(4x + 5)² = 625

Using the algebraic identity (a + b)2 we get 

(4x)² + 2(4x)(5) + 5² = 625

16x² + 40x + 25 = 625

Subtracting 625 on both sides, we get

16x² + 40x -600 = 0

2x² + 5x - 75 = 0

(x - 5) (2x + 15) = 0

Equating each factor to zero, we get

x = 5 and x = -15/2

By applying -15/2, we get the side length with negative sign, so the answer is 5.

Problem 11 :

The value of (68.237)² - (31.763)² is :

a)  3.6474     b)  36.474      c) 364.74      d)  3647.4

Solution :

= (68.237)² - (31.763)²

a² - b² = (a + b)(a - b)

= (68.237 + 31.763)(68.237 - 31.763)

= 100(36.474)

= 3647.4

So, option d is correct.

Problem 12 :

[(856 + 167)² + (856 - 167)²] / (856 x 856 + 167 x 167) = ?

a)  1    b)  2      c) 689      d)  1023

Solution :

= [(856 + 167)² + (856 - 167)²] / (856 x 856 + 167 x 167)

= (856² + 167² + 2(856)(167) + 856² + 167² - 2(856)(167)) / (856² + 167²)

= (856² + 167² + 856² + 167²) / (856² + 167²)

= 2(856²) + 2(167²) / (856² + 167²)

= 2 [(856² + 167²) / (856² + 167²)]

= 2

So, option b is correct.

Problem 12 :

Expand and simplify (a - 3)² - 3(a + 1)

Solution :

= (a - 3)² - 3(a + 1)

Using (a - b)² = a² - 2ab + b²

(a - 3)² = a² - 2(a)(3) + 3²

= a² - 6a + 9

Applying this expansion, we get

= a² - 6a + 9 - 3(a + 1)

= a² - 6a + 9 - 3a - 3

= a² - 9a + 6

Problem 13 :

Find the simplest expression for the shaded area of each figure.

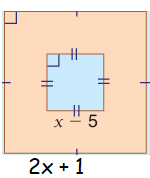
Solution :

The blue region is the shaded region. To find area of the middle part, we have to find the difference of area of large square and small square.

Side length of large square = 2x + 1

Side length of small square = x - 5

Area of blue region = (2x + 1)² - (x - 5)²

= (2x)² + 2(2x) (1) + 1² -  [x² - 2(x) (5) + 5²]

= 4x² + 4x + 1 -  [x² - 10x + 25]

= 4x² + 4x + 1 -  x² + 10x - 25

= 4x² -  x² + 4x + 10x + 1 - 25

= 3x² + 14x - 24