FINDING UNKNOWN WHEN THE GIVEN PIECEWISE FUNCTION IS CONTINUOUS

Find a that would make the function continuous.

Problem 1 :

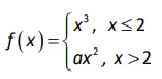
Solution :

Lim _x->2-  f(x) = Lim _x->2-  x³

Applying the limit, we get

Lim _x->2-  f(x) = (2)³

= 8 ----(1)

Lim _x->2+  f(x) = Lim _x->2+ ax²

Applying the limit, we get

Lim _x->2+  f(x) = a(2)²

= 4a----(2)

(1) = (2)

8 = 4a

a = 8/4

a = 2

Problem 2 :

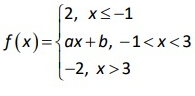
Solution :

lim _x->-1-  f(x) = Lim _x->-1- 2

Applying the limit, we get

Lim _x->-1-  f(x) = 2

Lim _x->-1+  f(x) = Lim _x->-1+ ax + b

Applying the limit, we get

Lim _x->-1+  f(x) = a(-1) + b

= -a + b

Equating left hand limit and right hand limit, we get

-a + b = 2 ----(1)

lim _x->3-  f(x) = Lim _x->3- ax + b

Applying the limit, we get

Lim _x->3-  f(x) = a(3) + b

= 3a + b

Lim _x->3+  f(x) = Lim _x->3+ -2

Applying the limit, we get

Lim _x->3+  f(x) = -2

Equating the left hand limit and right hand limit, we get

3a + b = -2 ----(2)

(1) - (2)

-a + b - (3a + b) = 2 + 2

-a + b - 3a - b = 4

-4a = 4

a = -4/4

a = -1

Applying the value of a in (1), we get

1 + b = 2

b = 2 - 1

b = 1

Problem 3 :

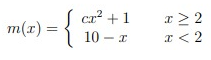
For which value of c is m(x) a continuous function ?

Solution :

Lim _x->2+  f(x) = Lim _x->2+  cx² + 1

Applying the limit, we get

Lim x->2⁺  f(x) = c(2)² + 1

= 4c + 1 ----(1)

Lim _x->2-  f(x) = Lim _x->2- 10 - x

Applying the limit, we get

Lim _x->2-  f(x) = 10 - 2

= 8 ----(2)

Since, m(x) is a continuous function.

Lim _x->2+  f(x) = Lim _x->2-  f(x) = Lim _x->2 f(x)

(1) = (2)

4c + 1 = 8

4c = 8 - 1

4c = 7

c = 7/4

For each of the following functions, find the values of the unknown variables that make each function continuous everywhere.

Problem 4 :

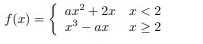
Solution :

Lim _x->2-  f(x) = Lim _x->2-  ax² + 2x

Applying the limit, we get

Lim _x->2-  f(x) = a(2)² + 2(2)

= 4a + 4 ----(1)

Lim _x->2+  f(x) = Lim _x->2+ x³ - ax

Applying the limit, we get

Lim x->2⁺  f(x) = (2)³ - 2a

= 8 - 2a ---- (2)

(1) = (2)

4a + 4 = 8 - 2a

4a + 2a = 8 - 4

6a = 4

a = 4/6

a = 2/3

Problem 5 :

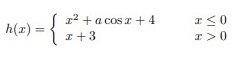
Solution :

Lim _x->0-  f(x) = Lim _x->0-  x² + a cos x + 4

Applying the limit, we get

Lim _x->0-  f(x) = a cos 0 + 4

= a + 4 ----(1)

Lim _x->0+  f(x) = Lim _x->0+ x + 3

Applying the limit, we get

Lim _x->0+  f(x) = 0 + 3 

= 3---- (2)

(1) = (2)

a + 4 = 3

a = 3 - 4

a = 1

Problem 6 :

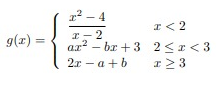
Solution :

lim _x->2-  g(x) = Lim _x->2- (x² - 4)/(x - 2)

lim _x->2-  g(x) = Lim _x->2- (x² - 2²)/(x - 2)

lim _x->2-  g(x) = Lim _x->2- (x - 2)(x + 2)/(x - 2)

lim _x->2-  g(x) = Lim _x->2- (x + 2)

Applying the limit, we get

Lim _x->-2-  g(x) = 2  + 2

Lim _x->-2-  g(x) = 4

Lim _x->2+  g(x) = Lim _x->2+ ax² - bx + 3

Applying the limit, we get

Lim _x->2+  g(x) =a(2)² - b(2) + 3

= 4a - 2b + 3

Equating left hand limit and right hand limit, we get

4a - 2b + 3 = 4

4a - 2b = 4 - 3

4a - 2b = 1--- (1)

lim _x->3-  g(x) = Lim _x->3- ax² - bx + 3

Applying the limit, we get

Lim _x->3-  g(x) = a(3²) - 3b + 3

= 9a - 3b + 3

Lim _x->3+  g(x) = Lim _x->3+ 2x - a + b

Applying the limit, we get

Lim _x->3+  g(x) = 2(3) - a + b

= 6 - a + b

Equating the left hand limit and right hand limit, we get

9a - 3b + 3 = 6 - a + b

9a - 3b - (-a + b) = 6 - 3

9a - 3b + a - b = 3

10a - 4b = 3 --- (2)

4a - 2b = 1 ----(1)

10a - 4b - 2(4a - 2b) = 3 - 2 

10a - 4b - 8a + 4b = 1

2a = 1

a = 1/2

Applying the value of a in (1), we get

4(1/2) - 2b = 1

2 - 2b = 1

1 = 2b

b = 1/2