FINDING UNKNOWN LENGTH BY PYTHAGOREAN THEOREM
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
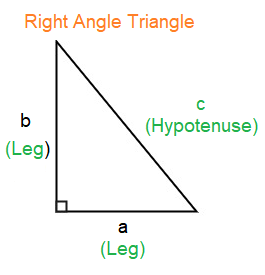
Pythagorean Theorem :
In any right angled triangle, the length of square of hypotenuse is equal to the sum of the squares on the other two sides
In a right angled triangle, with hypotenuse c and legs a and b,
c2 = a2 + b2
Find the unknown lengths :
Problem 1 :
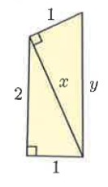
Solution :
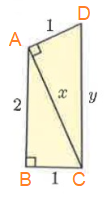
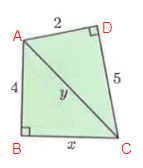
In figure ∆ABC and ∆DAC.
AB = 2, BC = 1 and AC = x
DA = 1, AC = √5 and DC = y
Using Pythagoras theorem :
|
In ∆ABC, AB² + BC² = AC² 2² + 1² = x² 4 + 1 = x² x² = 5 x = √5 |
In ∆DAC, DA² + AC² = DC² 1² + √5² = y² 1 + 5 = y² y² = 6
y = √6 |
So, x = √5 and y = √6.
Problem 2 :
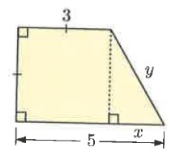
Solution :
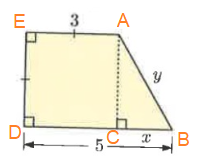
In figure BD = 5, AE = 3
BC = BD - AE
BC = 5 - 3
BC = 2
In ∆ABC,
AC = 3, BC = 2 and AB = y
By using Pythagoras theorem,
AC² + BC² = AB²
3² + 2² = y²
9 + 4 = y²
y² = 13
y = √13
So, x = 2 and y = √13.
Problem 3 :
Solution :
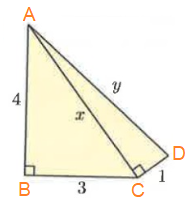
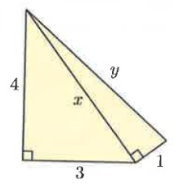
In figure ∆ABC and ∆ACD.
AB = 4, BC = 3 and AC = x
AC = 5, CD = 1 and AD = y
Using Pythagoras theorem :
|
In ∆ABC, AB² + BC² = AC² 4² + 3² = x² 16 + 9 = x² x² = 25
x = 5 |
In ∆ACD, AC² + CD² = AD² 5² + 1² = y² 25 + 1 = y² y² = 26
y = √26 |
So, x = 5 and y = √26.
Problem 4 :
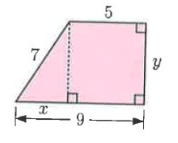
Solution :
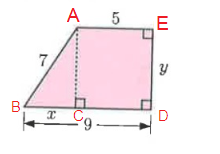
In figure BD = 9, AE = 5.
BC = BD - AE
BC = 9 - 5
BC = 4
In figure ∆ABC
In ∆ABC,
AB = 7, BC = 4 and AC = y
By using Pythagoras theorem
AC² + BC² = AB²
y² + 4² = 7²
y² + 16 = 49
y² = 49 - 16
y² = 33
y = √33
So, x = 4 and y = √33.
Problem 5 :
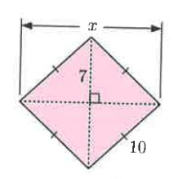
Solution:
In figure ∆ABC.
In ∆ABC,
AB = 7, AC = 10 and BC = x
By using Pythagoras theorem,
AB² + BC² = AC²
7² + x² = 10²
x² = 100 - 49
x² = 51
x = √51
EC = 2x
x = 2√51
Problem 6 :
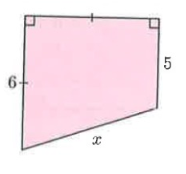
Solution :
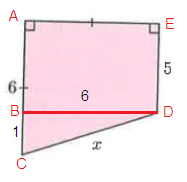
In figure ∆BCD.
In ∆BCD,
BC = 1, BD = 6 and CD = x
By using Pythagoras theorem
BC² + BD² = CD²
1² + 6² = x²
1 + 36 = x²
x² = 37
x = √37
Problem 7 :
Solution :
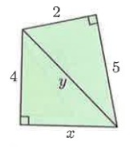
In figure ∆ABC and ∆ACD.
AD = 2, CD = 5 and AC = y
AB = 4, AC = √29 and BC = x
By using Pythagoras theorem,
|
In ∆ACD, AD² + CD² = AC² 2² + 5² = y² 4 + 25 = y² y² = 29 y = √29 |
In ∆ABC, AB² + BC² = AC² 4² + x² = (√29)² 16 + x² = 29 x² = 29 - 16 x² = 13 x = √13 |
So, x = √13 and y = √29.
Problem 8 :
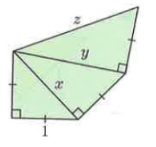
Solution :
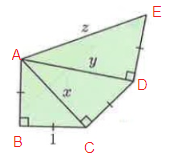
In figure ∆ABC, ∆ACD and ∆ADE.
AB = 1, BC = 1, AC = x, CD = 1, AD = y, DE = 1, and AE = z
By using Pythagoras theorem,
|
In ∆ABC, AB² + BC² = AC² 1² + 1² = x² x² = 1 + 1 x² = 2
x = √2 |
In ∆ACD, AC² + CD² = AD² (√2)² + 1² = y² 2 + 1 = y² y² = 3
y = √3 |
In ∆ADE, AD² + DE² = AE² (√3)² + 1² = z² 3 + 1 = z² z² = 4
z = 2 |
So, x = √2, y = √3 and z = 2.
Problem 9 :
ABC is an isosceles triangle
a) Find h
b) Find the area of the triangle.
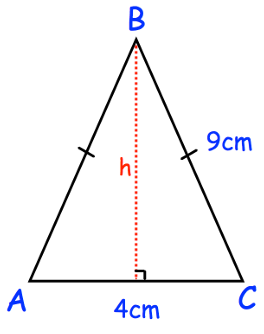
Solution :
In triangle ABC, AB = BC = 9 cm
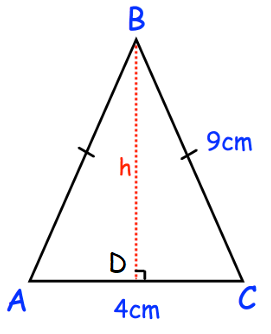
a)
DC = 2 cm
In triangle BDC,
BC2 = BD2 + DC2
92 = h2 + 22
h2 = 81 - 4
h2 = 77
h = √77
b)
Area of triangle = (1/2) x base x height
= (1/2) x √77 x 4
= 2 √77 cm2
Problem 10 :
A gardener marks out a new lawn that is supposed to be a rectangle with sides of length 8 m and 12 m. He checks that he has marked out a rectangle by measuring the diagonal. How long should be the diagonal be correct 1 decimal place.
Solution :
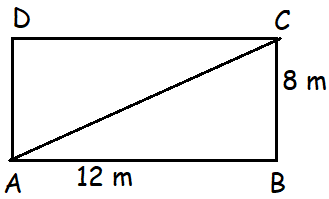
Using Pythagorean theorem,
AC2 = AB2 + BC2
AC2 = 122 + 62
AC2 = 144 + 36
= 180
AC = √180
= 13.41
Approximately 13.4 cm.
Problem 11 :
A ladder leans against a vertical wall. The length of the ladder is 6 m. The bottom of the ladder is 2 m from the base of the wall. How high is the top of the ladder above the ground ?
Solution :
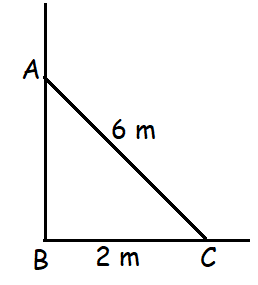
AC2 = AB2 + BC2
Let AB = x
62 = x2 + 22
36 = x2 + 4
x2 = 36 - 4
x2 = 32
AB = √32
Approximately 5.65 m
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling