FINDING UNKNOWN COEFFICIENTS IN CONTINUOUS FUCNTION

Problem 1 :

Find the value of a if the function is continuous.

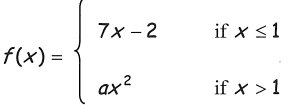
Solution :

Lim _x->1^-  f(x) = Lim _x->1^- 7x - 2

Applying the limit, we get

Lim _x->1^-  f(x) = 7(1) - 2

= 5 ----(1)

Lim _x->1⁺  f(x) = Lim _x->1⁺ ax²

Applying the limit, we get

Lim _x->1⁺  f(x) = a(1)²

= a----(2)

(1) = (2)

a = 5

Problem 2 :

Find the value of a if the function is continuous.

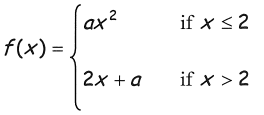
Solution :

Lim _x->2^-  f(x) = Lim _x->2^- ax²

Applying the limit, we get

Lim _x->2^-  f(x) = a(2)²

= 4a ----(1)

Lim _x->2⁺  f(x) = Lim _x->2⁺ 2x + a

Applying the limit, we get

Lim _x->2⁺  f(x) = 2(2) + a

= 4 + a----(2)

(1) = (2)

4a = 4 + a

4a - a = 4

3a = 4

a = 4/3

Problem 3 :

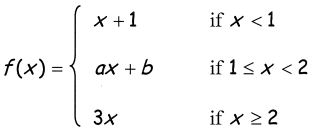
Solution :

lim _x->1^-  f(x) = Lim _x->1^- x + 1

Applying the limit, we get

Lim _x->1^-  f(x) = 1 + 1

= 2

Lim _x->1⁺  f(x) = Lim _x->1⁺ ax + b

Applying the limit, we get

Lim _x->1⁺  f(x) = a(1) + b

= a + b

Equating left hand limit and right hand limit, we get

a + b = 2 ----(1)

lim _x->2^-  f(x) = Lim _x->2^- ax + b

Applying the limit, we get

Lim _x->2^-  f(x) = a(2) + b

= 2a + b

Lim _x->2⁺  f(x) = Lim _x->2⁺ 3x

Applying the limit, we get

Lim _x->2⁺  f(x) = 3(2)

= 6

Equating the left hand limit and right hand limit, we get

2a + b = 6 ----(2)

(1) - (2)

a + b - (2a + b) = 2 - 6

-a = -4

a = 4

Applying the value of a in (1), we get

2(4) + b = 6

b = 6 - 8

b = -2

Problem 4 :

Find the values of a and b, if the function is continuous at x = 4.

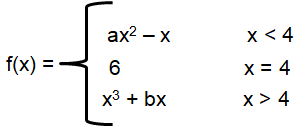
Solution :

Problem 5 :

Find the values of a and b, if the function is continuous for all x.

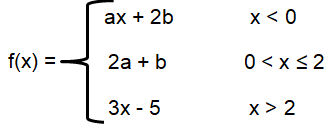
Solution :

(1) = (2)

2b = 2a + b

2b - b = 2a

b = 2a

(3) = (4)

2a + b = 1

Applying the value of b here, we get

2a + 2a = 1

4a = 1

a = 1/4

Applying the value of a in b = 2a

b = 2(1/4)

b = 1/2