FINDING UNKNOWN ANGLES IN A SUPPLEMENTARY PAIR
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
If the measure of two angles adds up to 180 degrees then the angles are called Supplementary Angles.
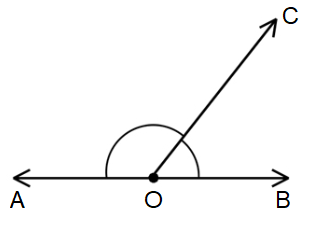
∠AOC + ∠COB = 180˚
Find the value of x in each supplementary angle pair.
Problem 1 :
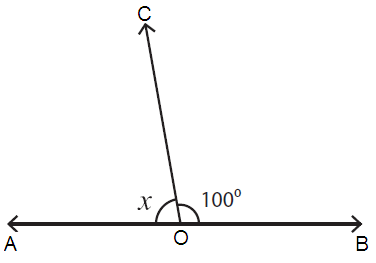
Solution :
The sum of the measures of supplementary angles = 180˚.
Here, ∠AOC = x and ∠COB = 100˚
∠AOC + ∠COB = 180˚
x + 100˚ = 180˚
x = 180˚ – 100˚
x = 80˚
So, the value of x is 80˚.
Problem 2 :
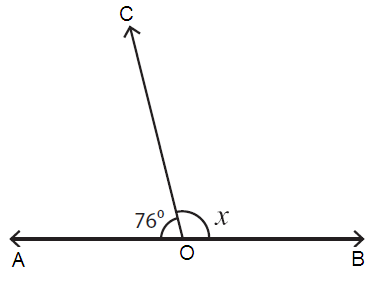
Solution :
The sum of the measures of supplementary angles = 180˚.
Here, ∠AOC = 76˚ and ∠COB = x
∠AOC + ∠COB = 180˚
76˚ + x = 180˚
x = 180˚ - 76˚
x = 104˚
So, the value of x is 104˚.
Problem 3 :
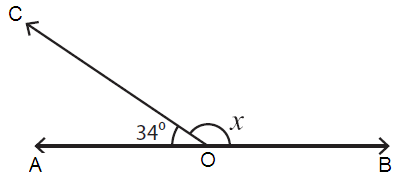
Solution :
The sum of the measures of supplementary angles = 180˚.
Here, ∠AOC = 34˚ and ∠COB = x
∠AOC + ∠COB = 180˚
34˚ + x = 180˚
x = 180˚ - 34˚
x = 146˚
So, the value of x is 146˚.
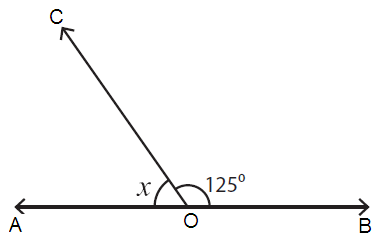
Problem 4 :
Solution :
The sum of the measures of supplementary angles = 180˚.
Here, ∠AOC = x and ∠COB = 125˚
∠AOC + ∠COB = 180˚
x + 125˚ = 180˚
x = 180˚ - 125˚
x = 55˚
So, the value of x is 55˚.
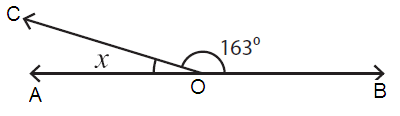
Problem 5 :
Solution :
The sum of the measures of supplementary angles = 180˚.
Here, ∠AOC = x and ∠COB = 163˚
∠AOC + ∠COB = 180˚
x + 163˚ = 180˚
x = 180˚ - 163˚
x = 17˚
So, the value of x is 17˚.
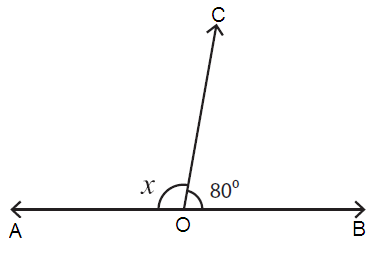
Problem 6 :
Solution :
The sum of the measures of supplementary angles = 180˚.
Here, ∠AOC = x and ∠COB = 180˚
∠AOC + ∠COB = 180˚
x + 80˚ = 180˚
x = 180˚ - 80˚
x = 100˚
So, the value of x is 100˚.
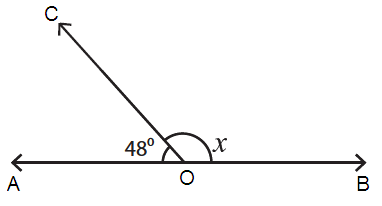
Problem 7 :
Solution :
The sum of the measures of supplementary angles =180˚.
Here, ∠AOC = 48˚ and ∠COB = x
∠AOC + ∠COB = 180˚
48˚ + x = 180˚
x = 180˚ - 48˚
x = 132˚
So, the value of x is 132˚.
Problem 8 :
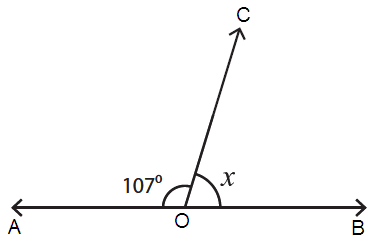
Solution :
The sum of the measures of supplementary angles = 180˚.
Here, <AOC = 107˚ and <COB = x
<AOC + <COB = 180˚
107˚ + x = 180˚
x = 180˚ - 107˚
x = 73˚
So, the value of x is 73˚.
Problem 9 :
Two angles form a linear pair. The measure of one angle is five times the measure of the other angle. Find the measure of each angle.
Solution :
Let x be the other angle. Then the first angle will be 5x.
It forms a linear pair, then sum of these angles will be 180 degree.
x + 5x = 180
6x = 180
x = 180/6
x = 30
5x = 5(30) ==> 150
So, the required angles are 30 and 150.
Problem 10 :
Find the measure of each angle, ∠EFG and ∠LMN are supplementary angles, m∠EFG = (3x + 17)°, and m∠LMN = ((1/2) x − 5)°
Solution :
Since the given angles are supplementary, sum of their angles must be 180 degree.
m∠EFG + m∠LMN = 180
3x + 17 + (1/2) x − 5 = 180
3x + x/2 + 12 = 180
3x + x/2 = 180 - 12
(6x + x)/2 = 168
7x/2 = 168
x = 168(2/7)
x = 48
|
m∠EFG = (3x + 17)° = 3(48) + 17 = 144 + 17 = 161 |
m∠LMN = ((1/2) x − 5)° = (1/2) (48) - 5 = 24 - 5 = 19 |
Problem 11 :
Find the angle measure if ∠5 is a supplement of ∠6, and m∠5 = 78°. Find m∠6.
Solution :
m∠5 + m∠6 = 180
78 + m∠6 = 180
m∠6 = 180 - 78
m∠6 = 102
Problem 12 :
Find the angle measure if ∠7 is a supplement of ∠8, and m∠7 = 109°. Find m∠8.
Solution :
m∠7 + m∠8 = 180
109 + m∠8 = 180
m∠8 = 180 - 109
m∠8 = 71
Problem 13 :
Find the measure of each angle.
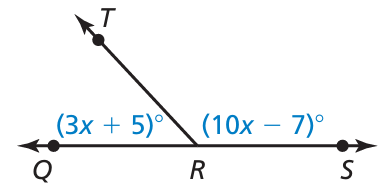
Solution :
m∠QRT + m∠TRS = 180
3x + 5 + 10x - 7 = 180
13x - 2 = 180
13x = 180 + 2
13x = 182
x = 182/13
x = 14
|
m∠QRT = 3(14) + 5 = 42 + 5 = 47 |
m∠TRS = 10(14) - 7 = 140 - 7 = 133 |
Problem 14 :
The arm of a crossing gate moves 42° from a vertical position. How many more degrees does the arm have to move so that it is horizontal?

a) 42° b) 138° c) 48° d) 90°
Solution :
42 + 138 = 180
To make it as horizontal, we need 138 degree.
Write and solve an algebraic equation to find the measure of each angle based on the given description.
Problem 15 :
The measure of one angle is 3° more than 1/2 the measure of its supplement.
Solution :
Let x be the angle.
Its supplementary angle is 180 - x
x = 1/2(180 - x) + 3
x = 90 - x/2 + 3
x + x/2 = 93
3x/2 = 93
x = 93(2/3)
x = 31(2)
x = 62
Problem 16 :
Two angles form a linear pair. The measure of one angle is 15° less than 2/3 the measure of the other angle.
Solution :
Let x be the one angle.
The other angle = 2/3 of x - 15
(2x/3) - 15
Since these two angles are linear pair, the sum of the angles will be 180 degree.
x + (2x/3) - 15 = 180
(3x + 2x)/3 = 180 + 15
5x/3 = 195
x = 195(3/5)
= 117
Applying the value of x, we get
= 2(117)/3 - 15
= 78 - 15
= 63
So, the angles are 63 and 117.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling