FINDING UNKNOWN ANGLES IN A COMPLEMENTARY PAIR

If the measure of two angles adds up to 90 degrees then the angles are called Complementary Angles.

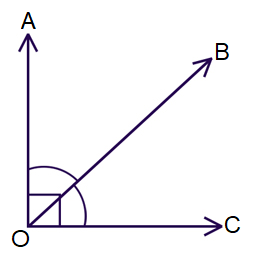
∠AOB + ∠BOC = 90˚

Find the value of x in each right angle.

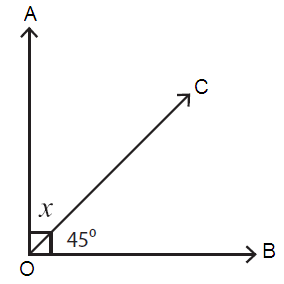
Problem 1 :

Solution :

The sum of the measures of complementary angles = 90˚.

Here, ∠AOC = x and ∠COB = 45˚

∠AOC + ∠COB = 90˚

x + 45˚ = 90˚

x = 90˚ – 45˚

x = 45˚

So, the value of x is 45˚.

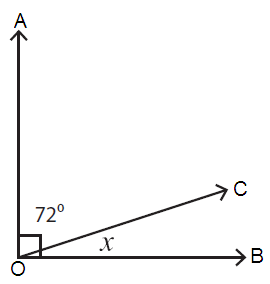
Problem 2 :

Solution :

The sum of the measures of complementary angles = 90˚.

Here, ∠AOC = 72˚ and ∠COB = x

∠AOC + ∠COB = 90˚

 72˚ + x = 90˚

x = 90˚ - 72˚

x = 18˚

So, the value of x is 18˚.

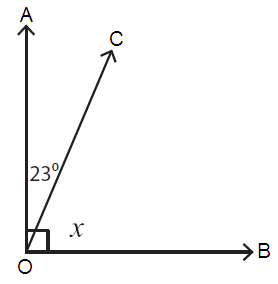
Problem 3 :

Solution :

The sum of the measures of complementary angles = 90˚.

Here, ∠AOC = 23˚ and ∠COB = x

∠AOC + ∠COB = 90˚

23˚ + x = 90˚

x = 90˚ - 23˚

x = 67˚

So, the value of x is 67˚.

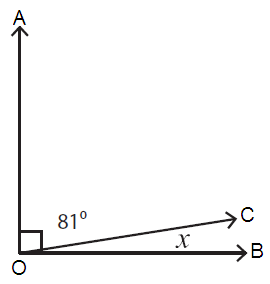
Problem 4 :

Solution :

The sum of the measures of complementary angles = 90˚

Here, ∠AOC = 81˚ and ∠COB = x

∠AOC + ∠COB = 90˚

81˚ + x = 90˚

x = 90˚ - 81˚

x = 9˚

So, the value of x is 9˚.

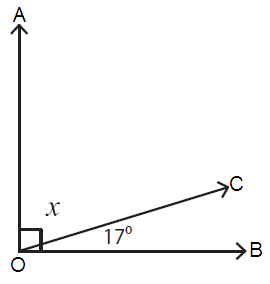
Problem 5 :

Solution :

The sum of the measures of complementary angles = 90˚.

Here, ∠AOC = x and ∠COB = 17˚

∠AOC + ∠COB = 90˚

x + 17˚= 90˚

x = 90˚ - 17˚

x = 73˚

So, the value of x is 73˚.

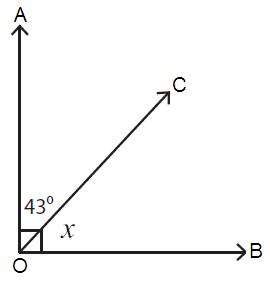
Problem 6 :

Solution :

The sum of the measures of complementary angles = 90˚.

Here, ∠AOC = 43˚ and ∠COB = x

∠AOC + ∠COB = 90˚

43˚ + x = 90˚

x = 90˚ - 43˚

x = 47˚

So, the value of x is 47˚.

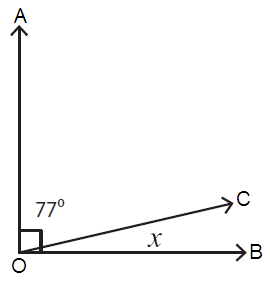
Problem 7 :

Solution :

The sum of the measures of complementary angles = 90˚.

Here, ∠AOC = 77˚and ∠COB = x

∠AOC + ∠COB = 90˚

77˚ + x = 90˚

x = 90˚ - 77˚

x = 13˚

So, the value of x is 13˚.

Problem 8 :

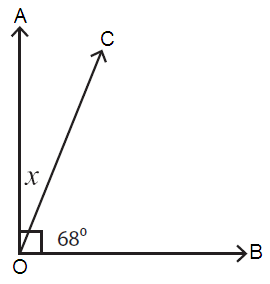
Solution :

The sum of the measures of complementary angles = 90˚.

Here, ∠AOC = x and ∠COB = 68˚

∠AOC + ∠COB = 90˚

x + 68˚ = 90˚

x = 90˚ - 68˚

x = 22˚

So, the value of x is 22˚.

Problem 9 :

When viewed from the side, the frame of a ball-return net forms a pair of supplementary angles with the ground. Find m∠BCE and m∠ECD.

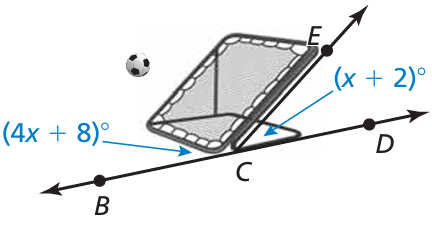
Solution :

∠BCE = 4x + 8

∠ECD = x + 2

∠BCE + ∠ECD = 180

4x + 8 + x + 2 = 180

5x + 10 = 180

5x = 180 - 10

5x = 170

x = 170/5

x = 34

Applying the value of x, 

• ∠BCE = 4(34) + 8 ==> 136 + 8 ==> 144
• ∠ECD = 34 + 2 ==> 36

Problem 10 :

∠LMN and ∠PQR are complementary angles. Find the measures of the angles when m∠LMN = (4x − 2)° and m∠PQR = (9x + 1)°.

Solution :

Since m∠LMN and m∠PQR are complementary angles, then their sum will become 90 degree.

m∠LMN + m∠PQR = 90

(4x − 2)° + (9x + 1)° = 90

13x - 1 = 90

13x = 90 + 1

13x = 91

x = 91/13

x = 7

Applying the value of x, we get

Problem 11 :

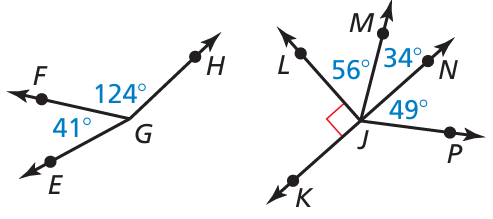
a) Name a pair of adjacent complementary angles.

b) Name a pair of adjacent supplementary angles.

Solution :

a) Complementary angles :

If the sum of two angles is 90 degree, then they are complementary angles.

∠LJM and ∠MJN

are adjacent complementary angles.

b) ∠KJL and ∠LJN are supplementray angles.

Find the measure of each angle.

Problem 12 :

Two angles form a linear pair. The measure of one angle is twice the measure of the other angle.

Solution :

Let x be the measure of other angle, the measure of one angle will be 2x. For linear pair, the sum of pairs of angles will be 180.

2x + x = 180

3x = 180

x = 180/3

x = 60

Problem 13 :

Two angles form a linear pair. The measure of one angle is 1/3 the measure of the other angle.

Solution :

Let x be the measure of other angle, then one angle will be 1/3 of x

x + 1/3 of x = 180

x + x/3 = 180

(3x + x)/3 = 180

4x/3 = 180

x = 180 (3/4)

x = 135

1/3 of x = 135/3 ==> 45

So, the required angles are 45 and 135.

Problem 14 :

The measure of an angle is nine times the measure of its complement.

Solution :

Let x be the measure of an angle.

The other angle = 9(90 - x)

x = 9(90 - x)

x = 810 - 9x

x + 9x = 810

10x = 810

x = 810/10

x = 81

90 - x ==> 90 - 81 ==> 9

So, the required angles are 9 and 81.