FINDING THE AREA OF COMPOSITE FIGURE

Find the area of each figure. Round to the nearest tenth if necessary.

Problem 1 :

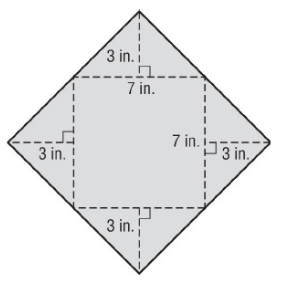
Solution :

Here, 4 triangles and 1 square.

Given, base = 7 in and Height = 3 in

Area of triangle = 1/2 × base × height

= 1/2 × 7 × 3

= 21 in²

 Area of 4 triangles = 4 × 21

 Area of 4 triangles = 84 in² --- > (1)

Area of square = a²

= (7)²

Area of square = 49 in² --- > (2)

Add (1) & (2), we get

= 84 + 49

= 133 in²

Problem 2 :

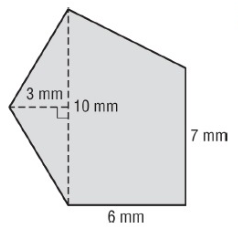
Solution :

Here, one triangle and one trapezoid.

Base = 10 mm , height = 3 mm

Area of triangle = 1/2 × base × height

= 1/2 × 10 × 3

Area of triangle = 15 mm² --- > (1)

a = 10 mm, b = 7 mm and h = 6 mm

Area of trapezoid = 1/2 × (a + b) h

= 1/2 × (10 + 7) × 6

= 1/2 × 102

Area of parallelogram = 51 mm² --- > (2)

Add (1) & (2)

= 15 + 51

= 66 mm²

Problem 3 :

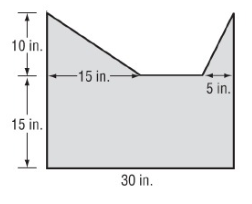
Solution :

Here 1 rectangle and 2 triangles.

Length = 15 in, width = 30 in

Area of rectangle A = length × width

= 15 × 30

= 450 in² --- > (1)

Base = 15 in, height = 10 in

Area of right triangle = 1/2 × b × h

= 1/2 × 15 × 10

= 75 in² --- > (2)

Base = 5 in, height = 10 in

Area of left triangle = 1/2 × b × h

= 1/2 × 5 × 10

= 25 in² --- > (3)

Add (1), (2) and (3), we get

Area = 450 + 75 + 25

Area = 550 in²

Problem 4 :

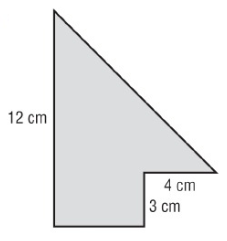
Solution :

Here 1 rectangle and 1 triangle.

Base = 9 cm, height = 9 cm

Area of triangle = 1/2 × b × h

= 1/2 × 9 × 9

= 40.5 cm² --- > (1)

Length = 3 cm, width = 5 cm

Area of rectangle = length × width

= 3 × 5

= 15 cm² --- > (2)

Add (1) & (2), we get

Area = 40.5 + 15

Area = 55.5 cm²

Problem 5 :

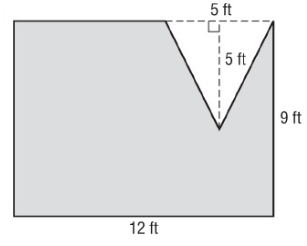
Solution :

Length = 12 ft, width = 9 ft

Area of rectangle = length × width

= 12 × 9

A₁ = 108 ft² --- > (1)

Base = 5 ft, height = 5 ft

Area of triangle = 1/2 × b × h

= 1/2 × 5 × 5

A₂ = 12.5 ft² --- > (2)

So, area of shaded part

Area = A₁ - A₂

Area = 108 - 12.5

Area = 95.5 ft²

Problem 6 :

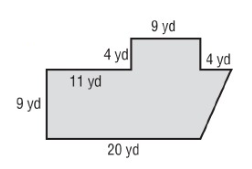
Solution :

Here 1 rectangle, 1 trapezoid and 1 triangle.

a = 24 yd, b = 20 yd, and h = 9 yd

Area of trapezoid = 1/2 × (a + b) h

= 1/2 × (24 + 20) × 9

= 1/2 × 44 × 9

Area = 198 yd²

Length = 9 yd, width = 4 yd

Area of rectangle A₂ = length × width

= 9 × 4

A₂ = 36 yd² --- > (2)

Base = 4 yd, height = 9 yd

Area of triangle = 1/2 × b × h

= 1/2 × 4 × 9

= 18 yd² --- > (3)

Add (1), (2) & (3), we get

Area = 198 + 36 + 18

Area = 252 yd²

Problem 7 :

How many times greater is the area of the floor covered by the larger speaker than by the smaller speaker?

Solution :

Area covered by large speaker = (1/2) x 2h x (2b₁ + 2b₂)

= h(2b₁ + 2b₂)

Area covered by small speaker = (1/2) x h x (b₁ + b₂)

= (1/2)h(b₁ + b₂)

Number of times = h(2b₁ + 2b₂) / (1/2)h(b₁ + b₂)

= 2

So, the required number of times is 2.

Problem 8 :

The stained-glass window is made of identical kite-shaped glass panes. Th e approximate dimensions of one pane are shown. The glass used to make the window costs $12.50 per square foot. Find the total cost of the glass used to make the window.

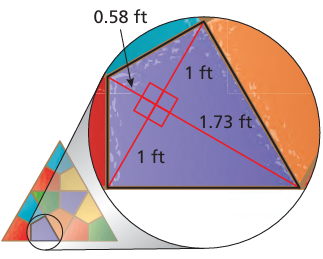
Solution :

To make a window we need 12 glasses.

Area of triangles at the left side = 2 x (1/2) x 0.58 x 1

= 0.58 square feet

Area of triangles at the right side = 2 x 1/2 x 1.73 x 1

= 1.73 square feet

Total area = 0.58 + 1.73

= 2.31 square feet

Area of window = 12 x 2.31

= 27.72 square feet

Cost per m² = $12.50

Required cost = 12.50 x 27.72

= $346.5

Problem 9 :

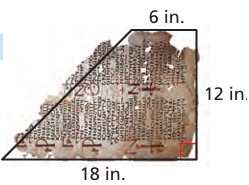
An archaeologist estimates that the manuscript shown was originally a rectangle with a length of 20 inches. Estimate the area of the fragment that is missing.

Solution :

The given shape looks like a trapezium.

base (a) = 18 inches, base (b) = 6 inches and height (h) = 12 inches

Area of trapezium = (1/2) x h (a + b)

= (1/2) x 12 x (18 + 6)

= 6 x 24

= 144 square inches