FINDING RECIPROCAL OF A NUMBER

Example 1 :

State the reciprocal of:

a) 3/4     b) 2/7     c)  4     d)  -1/2     e)  -2

f)  5/8     g)  -5/2     h)  -1     i)  0

Solution :

a) Reciprocal of 3/4 is 4/3.

b) Reciprocal of 2/7 is 7/2.

c) Reciprocal of 4 is 1/4.

d) Reciprocal of -1/2 is -2/1 that is -2.

e) Reciprocal of -2 is -1/2

f) Reciprocal of 5/8 is 8/5.

g) Reciprocal of -5/2 is -2/5.

h) Reciprocal of -1 is -1.

i) Reciprocal of 0 is undefined.

Example 2 :

4/7 of a number is 84. Find the number.

Solution :

4/7 of a number = 84 ----(1)

By finding 7/4 of the number, we can find that number.

Multiplying (1) by 7/4 on both sides.

(7/4) x (4/7) of a number = (7/4) x 84

Number = 7 x 21 ==> 147

So, the required number is 147.

Example 3 :

Find the quotient of 1/3 and 3/4.

Solution :

Let a = 1/3 and b = 3/4

To find the quotient of a and b, we have to divide a by b.

= (1/3) / (3/4)

If two fractions are divided, keep the first fraction as it is and change the division sign as multiplication and write the reciprocal of the second fraction.

= (1/3) x (4/3)

= 4/9

Example 4 :

Find the reciprocal of 5 and 7/8.

Solution :

Product of 5 and 7/8 = 5 x (7/8)

= 35/8

Reciprocal of 35/8 is 8/35.

Example 5 :

Write the reciprocal of the number.

a)  5/8    b)  6       c)  1/3       d)  7/4

Solution :

a)  5/8

By fliping the fraction, we get 8/5. So, the reciprocal of 5/8 is 8/5.

b)  6

By writing the integer as fraction, we get 6/1.

By fliping the fraction, we get 1/6. So, the reciprocal of 6 is 1/6.

c)  1/3

By fliping the fraction, we get 3/1. So, the reciprocal of 1/3 is 3/1 or 3.

d)  7/4

By fliping the fraction, we get 7/4. So, the reciprocal of 7/4 is 4/7.

Example 6 :

Write the answer in simplest form.

a)  1/6 ÷ 1/3

b)  3/4 ÷ 6

c)  3/5 ÷ 2/15

d)  10 ÷ 2/7

e)  3/8 ÷ 9/16

f)  5/9 ÷ 15

g) 7/12 ÷ 14

Solution :

a)  1/6 ÷ 1/3

= 1/6 ⋅ (3/1)

= 1/2

b)  3/4 ÷ 6

= 3/4 ÷ 6/1

= 3/4 ⋅ (1/6)

= 1/8

c)  3/5 ÷ 2/15

= 3/5 ⋅ (15/2)

= 9/2

d)  10 ÷ 2/7

= 10/1 ÷ 2/7 

= 10/1 ⋅ (7/2)

= 5 ⋅ 7

= 35

e)  3/8 ÷ 9/16

= 3/8 ⋅ 16/9

= 2/3

f)  5/9 ÷ 15

= 5/9 ÷ 15/1

= 5/9 ⋅ (1/15)

= 1/27

g) 7/12 ÷ 14

= 7/12 ÷ 14/1

= 7/12 ⋅ 1/14

= 1/24

Example 7 :

Describe and correct the error in finding the quotient.

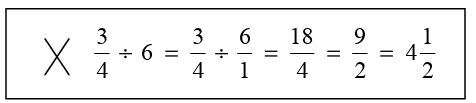
Solution :

When dividing fraction by another fraction, fraction by integer or integer by fraction, we have to write the first fraction as it is and change the division sign as multiplication and change the reciprocal of second fraction.

By observing the work given, the error is we should change the division sign as multiplication and write the reciprocal of 6/1, then will get

= 3/4 x 1/6

= 1/8

is the correct answer.

Example 8 :

Determine whether the numbers are reciprocals. If not, write the reciprocal of each number. 

a)  5/8, 16/10

b)  1/12, 12

c)  2/3, 12/18

d)  4/7, 7/8

Solution :

a)  5/8, 16/10

For 5/8, its reciprocal will be 8/5.

Finding the equivalent fraction for 8/5, we get 16/10. So, the given fractions are reciprocal to each.

b)  1/12, 12

For 1/12, its reciprocal will be 12/1 or 12.

So, the given fractions are reciprocal to each.

c)  2/3, 12/18

For 2/3, its reciprocal will be 3/2

Finding the equivalent fraction for 3/2, we get 6/4, 9/6, 12/8. So, the given fractions are not reciprocal to each.

d)  4/7, 7/8

For 4/7 its reciprocal is 7/4. By finding equivalent fraction for 7/4, we get 14/8. So, the given fractions are not reciprocal to each.

Example 9 :

Copy and complete the statement.

a)  10/7 x ? = 1

b)  8 ÷ ? = 24

Solution :

a) By multiplying a fraction by its reciprocal, we get 1. Then 10/7 x 7/10 will give 1. So, the required number is 7/10.

b) 8 ÷ ? = 24

Let x be the unknown

8 ÷ x = 24

8/x = 24

x = 8/24

x = 1/3

So, the required number is 1/3.

Example 10 :

You have 2/3 of a pizza. You divide the remaining pizza into 4 equal pieces. What fraction of the pizza is each piece?

Solution :

Quantity of pizza you have = 2/3

Dividing this part by four equal parts, we get

= 2/3 ÷ 4

= 2/3 ÷ 4/1

= 2/3 ⋅ (1/4)

= 1/6 part of pizza is each piece.

Example 11 :

You have five quarts of paint. It takes 5/8 quart to paint each chair you are asked to paint. How many chairs can you paint?

Solution :

Quantity of paint you have = 5 quarts

Each chair will consume 5/8 quart.

Number of chairs to be painted = 5 ÷ (5/8)

= 5 ⋅ (8/5)

= 8

So, the number of chairs to be painted is 8.

Example 12 :

Is the reciprocal of a fraction always a whole number? Explain.

Solution :

Yes, for example let us conside the fraction 1/7, its reciprocal will be 7/1 or 7. So, it is true sometimes.