FINDING MISSING DIAGONAL OF A RHOMBUS WORKSHEET

Find the length of the missing diagonal in each rhombus

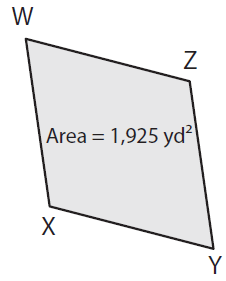
Problem 1 :

If WY = 70 yd, find XZ.

Solution

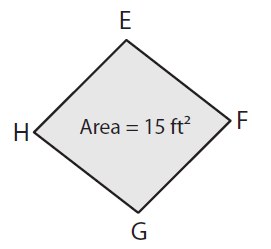
Problem 2 :

If FH = 6 ft, find EG.

Solution

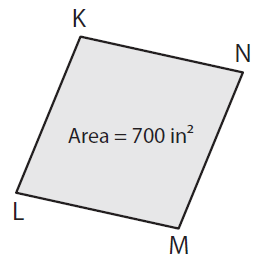
Problem 3 :

If KM = 35 in, find LN.

Solution

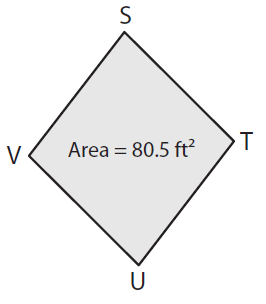
Problem 4 :

If VT = 7ft, find SU.

Solution

Problem 5 :

If BD = 16 in, find AC.

Solution

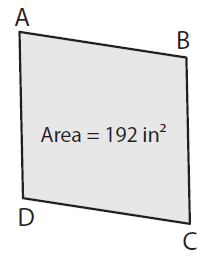
Problem 6 :

If VX = 49 yd, find UW.

Solution

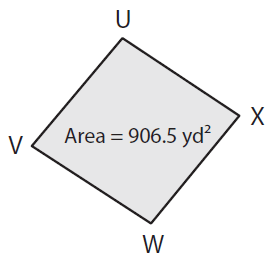
Problem 7 :

The length of one of the diagonal of a rhombus is 38 inches. Find the length of the other diagonal, if the area is 646 square inches.

Solution

Problem 8 :

The area of a rhombus is 125 square yards. If one of the diagonals measures 10 yards, find the length of the other diagonal.

Solution

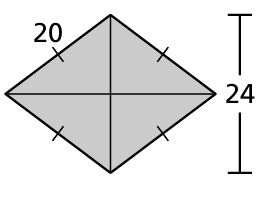
Problem 9 :

Find the area of the kite or rhombus

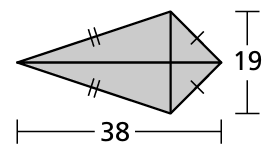
Problem 10 :

Find the area of the kite or rhombus.

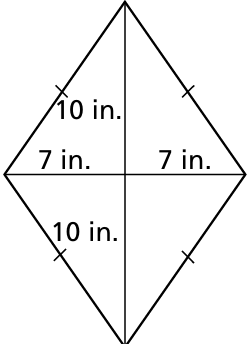
Problem 11 :

Find the area of the kite or rhombus.

Solution

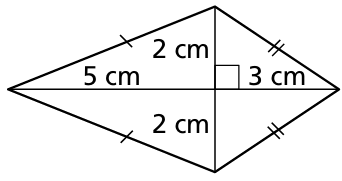
Problem 12 :

Find the area of the kite or rhombus.

Solution

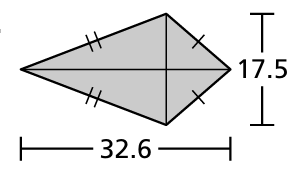
Problem 13 :

Solution

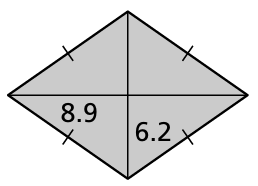
Problem 14 :

Solution

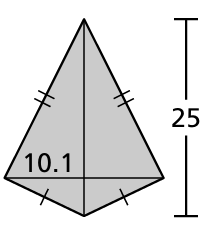
Problem 15 :

Solution

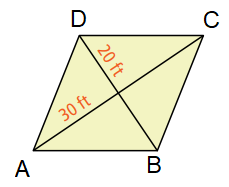
Problem 1 :

Find the side length of the rhombus ABCD.

Problem 2 :

The area of a rhombus is 150 cm². The length of one of its diagonal is 10 cm. The length of their other diagonal is .

(a)  25 cm   (b)  30 cm   (c) 35 cm    (d)  40 cm

Solution

Problem 3 :

One of the diagonals of a rhombus is double the other diagonal. Its area is 25 sq.cm. The sum of the diagonal is 

(a)  10 cm   (b)  12 cm   (c) 15 cm    (d)  16 cm

Solution

Problem 4 :

If the diagonals of a rhombus are 24 cm and 10 cm, find the area and perimeter of rhombus.

Solution

Problem 5 :

Each side of a rhombus is 26 cm and one of its diagonal is 48 cm long. The area of the rhombus is.

(a) 240 cm²       (b) 300 cm²  (c) 360 cm²    (d) 480 cm²

Solution

Problem 6 :

The length one diagonal of a rhombus is 80% of the other diagonal. The area of the rhombus is how many times the square of length of the other diagonal ?

(a) 4/5   (b)  2/5   (c)  3/4     (d)  1/4

Solution

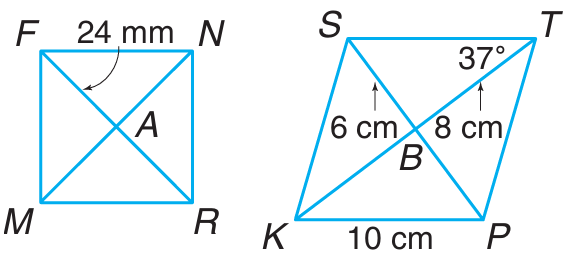
Problem 7 :

Use square FNRM or rhombus STPK to find each measure

Solution

Problem 8 :

The diagonals of a square are (x + 8) feet and 3x feet. Find the measure of the digonals.

Solution

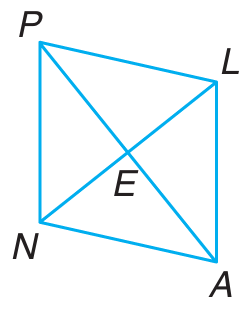
Problem 9 :

Refer to rhombus PLAN

a) Classify trangle PLA by its sides.

b)  Classify triangle PEN by its angles.

c) Is triangles PEN and triangle AEL congruent. Explain.

Solution

Problem 10 :

The area of a kite is 324 square inches. One diagonal is twice as long as the other diagonal. Find the length of each diagonal.

Solution

Problem 11 :

One diagonal of a rhombus is four times the length of the other diagonal. The area of the rhombus is 98 square feet. Find the length of each diagonal.

Solution