Finding Missing Angles in Triangles

Write and solve an equation to find the value of x for each of the triangle

Problem 1 :

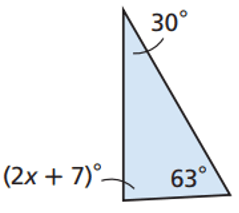
Solution :

Sum of the interior angles of the triangle = 180

2x + 7 + 63 + 30 = 180

2x + 100 = 180

Subtracting 100 on both sides.

2x = 180 - 100

2x = 80

Divide by 2 on both sides.

x = 40

Problem 2 :

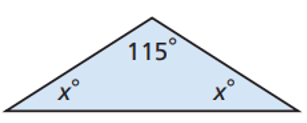
Solution :

Sum of interior angles = 180

115 + x + x = 180

2x + 115 = 180

Subtract 115 on both sides.

2x = 180 - 115

2x = 65

Divide it by 2.

x = 65/2

Problem 3 :

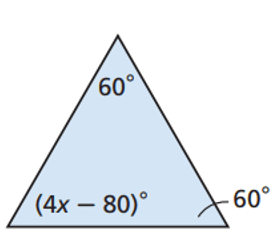
Solution:

60 + 60 + 4x - 80 = 180

120 + 4x - 80 = 180

40 + 4x = 180

Subtract 40 on both sides

4x = 180 - 40

4x = 140

Divide by 4 on both sides.

x = 140/4

x = 35

Problem 4 :

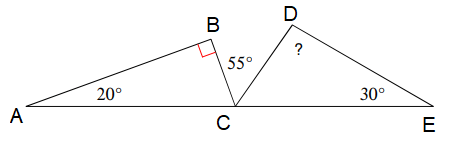
Solution :

∠A + ∠B + ∠BCA = 180

20 + 90 + ∠BCA = 180

∠BCA = 180 - 110

∠BCA = 70

∠BCD = 55

∠ACB + ∠BCD + ∠DCE = 180

70 + 55 + ∠DCE = 180

125 + ∠DCE = 180

Subtract 125 on both sides.

∠DCE = 180 - 125

∠DCE = 55

Problem 5 :

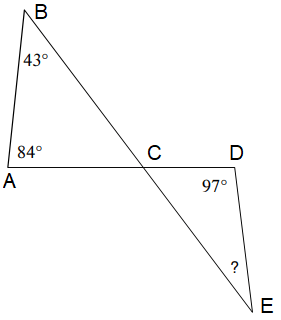
Solution :

∠A + ∠B + ∠ACB = 180

84 + 43 + ∠ACB = 180

127 + ∠ACB = 180

∠ACB = 180 - 127

∠ACB = 53

∠ACB = ∠CDE (vertically opposite angles)

∠CDE + ∠D + ∠E = 180

53 + 97 + ∠E = 180

150 + ∠E = 180

Subtract 150.

∠E = 180 - 150

∠E = 30

Problem 6 :

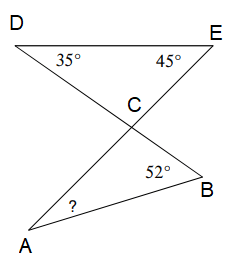
Solution :

∠DCE + ∠D + ∠E = 180

∠DCE + 35 + 45 = 180

∠DCE + 80 = 180

Subtract 80.

∠DCE = 180 - 80

∠DCE = 100

In triangle ACD.

∠DCE = ∠ACB = 100 (Vertically opposite angles)

∠ACB + ∠A + ∠B = 180

100 + ∠A + 52 = 180

152 + ∠A = 180

Subtracting 152 on both sides.

∠A = 180 - 152

∠A = 38

Problem 7 :

Find the measure of each acute angle in the right triangle. The measure of one acute angle is 5 times the measure of the other acute angle.

Solution :

Let x be the other acute angle.

One acute angle = 5x

x + 5x + 90 = 180

6x = 180 - 90

6x = 90

x = 90/6

x = 15

5(15) ==> 75

So, the acute angles are 15 and 75.

Problem 8 :

Find the measure of each acute angle in the right triangle.The measure of one acute angle is 8 times the measure of the other acute angle.

Solution :

Let x be the other acute angle.

One acute angle be 8x

x + 8x + 90 = 180

9x = 180 - 90

9x = 90

x = 90/9

x = 10

8x ==> 8(10) ==> 80

So, the acute angles are 10 and 80.

Problem 9 :

Find the measure of each acute angle in the right triangle. The measure of one acute angle is 3 times the sum of the measure of the other acute angle and 8.

Solution :

Let x be the other acute angle. One acute angle = 3 (x + 8)

x + 3(x + 8) + 90 = 180

x + 3x + 24 = 180 - 90

4x = 90 - 24

4x = 66

x = 66/4

x = 16.5

3(x + 8) ==> 3(16.5 + 8)

= 3(24.5)

= 73.5

So, the acute angles are 16.5 and 73.5.

Problem 10 :

Find the measure of each acute angle in the right triangle. The measure of one acute angle is twice the difference of the measure of the other acute angle and 12.

Solution :

Let x be the other acute angle.

One acute angle = 2(x - 12)

x + 2(x - 12) + 90 = 180

x + 2x - 24 + 90 = 180

3x + 66 = 180

3x = 180 - 66

3x = 114

x = 114/3

x = 38

2(x - 12) ==> 2(38 - 12)

= 2(26)

= 52

So, the acute angles are 38 and 52.

Problem 11 :

Find the measure of the numbered angle.

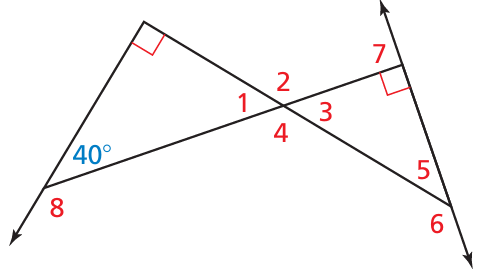
Solution :

∠8 + 40 = 180

∠8 = 180 - 40

∠8 = 140

In the triangle in the left,

40 + 90 + ∠1 = 180

130 + ∠1 = 180

∠1 = 180 - 130

∠1 = 50

∠3 = 50 (Vertically opposite angles)

∠3 + ∠4 = 180

50 + ∠4 = 180

∠4 = 180 - 50

∠4 = 130

∠4 = 130 (Vertically opposite angles)

In the triangle in the right,

∠3 + 90 + ∠5 = 180

50 + 90 + ∠5 = 180

140 + ∠5 = 180

∠5 = 180 - 140

∠5 = 40

∠6 = 180 - 40

∠6 = 140