FINDING INVERSE OF A FUNCTION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
To find the inverse of a function, write the function y as a function of x. To find inverse of a function, we have to follow the instruction
Step 1 :
Solve for x in the function.
Step 2 :
Write x as f-1(x) and replace y by x.
Find the
inverse of each function. Then graph the function and its inverse.
Problem 1 :
f(x) = x + 3
Solution :
f(x) = x + 3
In the above function f(x) to be replaced by ‘y’.
y = x + 3
Solve for x,
x = y - 3
Replace x by f-1(x) and y by x
f-1(x) = x - 3
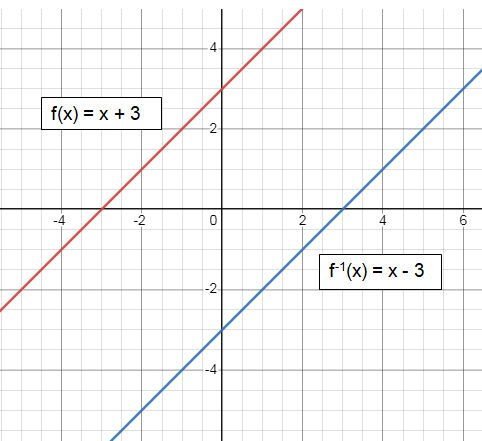
Problem 2 :
f(x) = (x - 2)/ 5
Solution:
Given function,
f(x) = (x - 2)/ 5
In the above function f(x) to be replaced by ‘y’.
y = (x - 2)/ 5
Solve for x,
5y = x - 2
x = 5y + 2
Replace x by f-1(x) and y by x
f-1(x) = 5x + 2
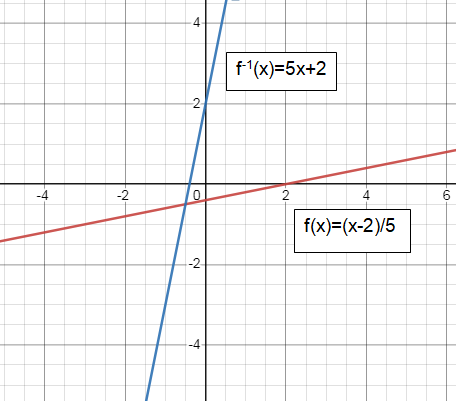
Problem 3 :
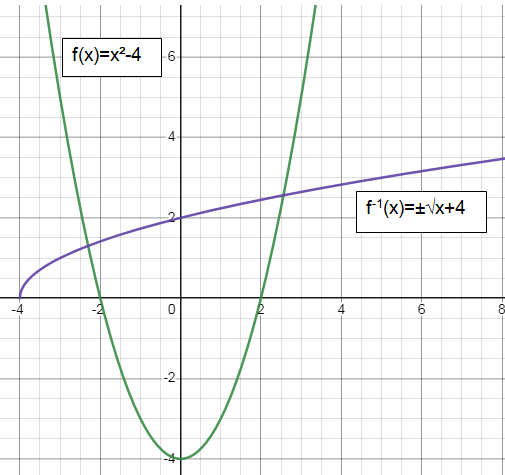
f(x) = x² - 4
Solution :
f(x) = x² - 4
In the above function f(x) to be replaced by ‘y’.
y = x² - 4
x² = y + 4
x = ± √y + 4
Replace x by f-1(x) and y by x
f-1(x) = ± √x + 4
Problem 4 :
f(x) = -7x - 9
Solution :
f(x) = -7x - 9
In the above function f(x) to be replaced by ‘y’.
y = -7x - 9
7x = -y - 9
x = (-y - 9)/7
Replace x by f-1(x) and y by x
f-1(x) = (-x - 9)/7
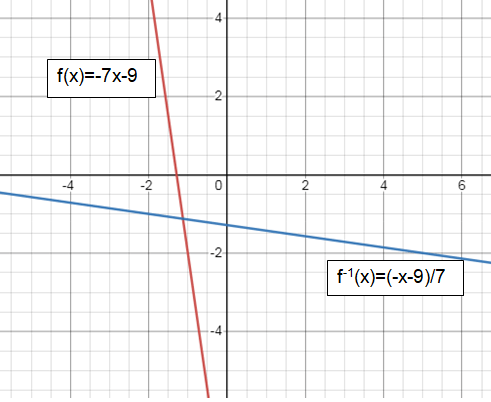
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling