FINDING EXPONENTIAL FUNCTION FROM TABLE

The table contains some points on the graph of an exponential function. Based on the table, what function represents the relationship

Problem 1 :

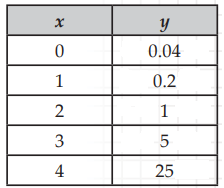
Solution :

Initial value (a) = 0.04

Check if the table represents exponential function or not :

0.2/0.04 ==> 5

1/0.2 ==> 5

5/1 ==> 5

25/5 ==> 5

Since common ratio is same, it is exponential function.

Here,

b = 5 > 1 (exponential growth)

y = 0.04(5)^x

Problem 2 :

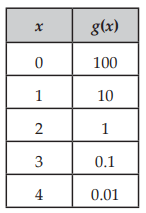
Solution :

Initial value (a) = 100

Check if the table represents exponential function or not :

10/100 ==> 1/10

1/10 ==> 1/10

0.1/1 ==> 1/10

0.01/0.1 ==> 1/10

Since common ratio is same, it is exponential function.

Here,

b = 0< 1/10 < 1  (exponential decay)

g(x) = 100(1/10)^x

Problem 3 :

Solution :

Initial value (a) = 2

Check if the table represents exponential function or not :

3/2 ==> 1.5

(9/2)/3  ==> 1.5

(27/4) / (9/2) ==> 1.5

(81/4) / (27/4) ==> 1.5

Since common ratio is same, it is exponential function.

Here,

b = 1.5 > 1 (exponential growth)

h(x) = 2(1.5)^x

Problem 4 :

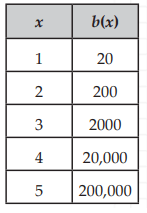
Solution :

Initial value is not given, when x = 0, there is no value for b(x). 

Check if the table represents exponential function or not :

200/20 ==> 10

2000/200  ==> 10

20000/2000 ==> 10

Since common ratio is same, it is exponential function.

Here,

b = 10 > 1 (exponential growth)

b(x) = a(10)^x ----(1)

Applying the point (1, 20) in the function, we get

20 = a(10)¹

a = 20/10

a = 2

Applying the value of a in (1), we get

b(x) = 2(10)^x

Problem 5 :

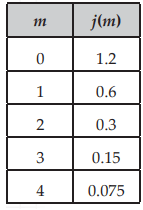
Solution :

Initial value a = 1.2

Check if the table represents exponential function or not :

0.6/1.2 ==> 0.5

0.3/0.6 ==> 0.5

0.15/0.3 ==> 0.5

0.075/0.15 ==> 0.5

Since common ratio is same, it is exponential function.

Here,

b = 0.5, 0 < b < 1 (exponential decay)

b(x) = 1.2(0.5)^x 

Problem 6 :

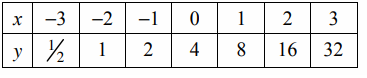
Solution :

Initial value is not given, when x = 0, y = 4

Check if the table represents exponential function or not :

1/(1/2) ==> 2

2/1  ==> 2

16/8 ==> 2

Since common ratio is same, it is exponential function.

Here,

b = 2 > 1 (exponential growth)

b(x) = 4(2)^x ----(1)

Problem 7 :

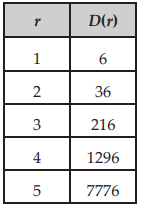
Solution :

Initial value is not given, when x = 0, there is no value for D(r). 

Check if the table represents exponential function or not :

36/6 ==> 6

216/36  ==> 6

1296/216 ==> 6

7776/1296 ==> 6

Since common ratio is same, it is exponential function.

Here,

b = 6 > 1 (exponential growth)

b(x) = a(10)^x ----(1)

Applying the point (1, 6) in the function, we get

6 = a(6)¹

a = 6/6

a = 1

Applying the value of a in (1), we get

D(r) = 1(6)^x

Problem 8 :

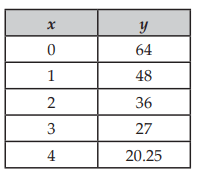
Solution :

Initial value is a = 64.

Check if the table represents exponential function or not :

48/64 ==> 0.75

36/48 ==> 0.75

27/36 ==> 0.75

20.25/27 ==> 0.75

Since common ratio is same, it is exponential function.

Here,

b = 0.75, 0 < b < 1 (exponential decay)

y = 64(0.75)^x