FINDING EQUATION OF PARABOLA FROM GRAPH

Find the equation of each of the following parabolas in the following forms.

i)  Vertex form

ii) Standard form

Problem 1 :

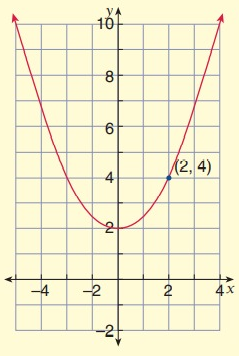
Solution:

Vertex Form:

Vertex form equation of a parabola that opens up with vertex (h, k)

y = a(x - h)² + k

Vertex (h, k) = (0, 2)

Substitute x = 2 and y = 4 in equation,

4 = a(2 - 0)² + 2 ----(1)

4 = a(4) + 2

4 = 4a + 2 

4a = 2

a = 1/2

applying the value of a in (1)

By applying a = 1/2 in equation,

y = 1/2 (x - 0)² + 2

y = 1/2 x² + 2

Standard Form:

The parabola is open up with vertex at (0, 2).

Standard form equation of a parabola that opens up with vertex at (0, 2)

(x - h)² = 4a(y - k)

Substitute x = 2 and y = 4 in equation,

(2 - 0)² = 4a(4 - 2)

4 = 4a(2)

4 = 8a

a = 1/2

By applying a = 1/2 in equation

(x - 0)² = 4(1/2)(y - 2)

x² = 2(y - 2)

x² = 2y - 4

x² - 2y + 4 = 0

Problem 2 :

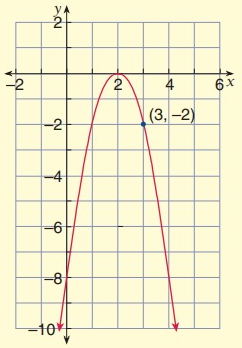
Solution:

Vertex form equation of a parabola that opens down with vertex (h, k)

y = a(x - h)² + k

Vertex (h, k) = (2, 0)

Substitute x = 3 and y = -2 in equation,

-2 = a(3 - 2)² + 0

-2 = a(1) + 0

a = -2   

By applying a = -2 in equation,

y = -2(x - 2)² + 0

Vertex form :

y = -2(x - 2)²

Standard Form:

y = -2(x - 2)²

y = -2 (x² - 2x(2) + 2²)

y = -2 (x² - 4x + 4)

y = -2x² + 8x - 8

Problem 3 :

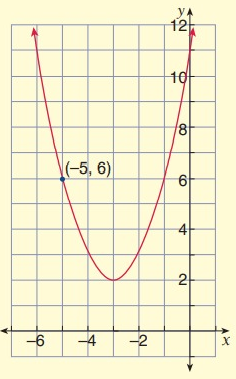
Solution:

Vertex form equation of a parabola that opens down with vertex (h, k)

y = a(x - h)² + k

Vertex (h, k) = (-3, 2)

Substitute x = -5 and y = 6 in equation,

6 = a(-5 + 3)² + 2

6 = a(4) + 2

6 = 4a + 2

4a = 4

a = 1

By applying a = 1 in equation,

y = 1 (x + 3)² + 2

Vertex form :

y = (x + 3)² + 2

Standard Form:

y = (x + 3)² + 2

Expanding (x + 3)² using algebraic identity, we get

y = x² + 2x(3) + 3² + 2

y = x² + 6x + 9 + 2

y = x² + 6x + 11

Find the equations of parabolas shown in the following forms :

i) Intercept form

ii) Standard form

Problem 4 :

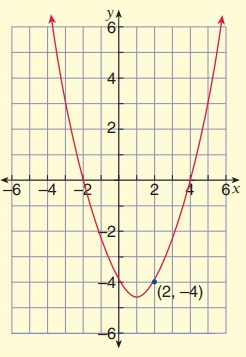
Solution:

Intercept Form:

Intercept form equation of the above parabola:

y = a(x - p) (x - q)

Because x-intercepts are (-2, 0) and (4, 0).

x = -2 ------> x + 2 = 0

x = 4 -------> x - 4 = 0

Then,

y = a(x + 2) (x - 4)

It passes through (2, -4). Substitute (x, y) = (2, -4)

-4 = a(2 + 2) (2 - 4)

-4 = a(4)(-2)

-4 = -8a

a = 1/2

Intercept form equation of the parabola:

y = 1/2(x + 2) (x - 4)

Standard form :

y = 1/2(x² - 4x + 2x - 8)

y = 1/2(x² - 2x - 8)

Problem 5 :

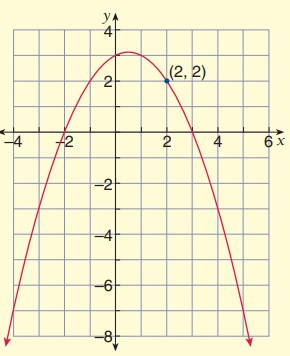
Solution:

Intercept Form:

Intercept form equation of the above parabola:

y = -a(x - p) (x - q)

Because x-intercepts are (-2, 0) and (3, 0).

x = -2 ------> x + 2 = 0

x = 3 -------> x - 3 = 0

Then,

y = -a(x + 2) (x - 3)

It passes through (2, 2). Substitute (x, y) = (2, 2)

2 = -a(2 + 2) (2 - 3)

2 = -a(4)(-1)

2 = 4a

a = 1/2

Intercept form equation of the parabola:

y = -1/2(x + 2) (x - 3)

Standard form :

y = -1/2(x² - 3x + 2x - 6)

y = -1/2(x² - x - 6)

Problem 6 :

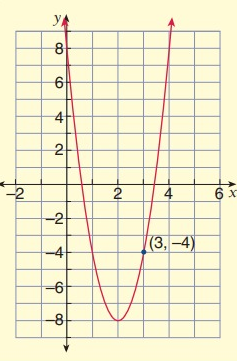
Solution:

Vertex Form:

Vertex form equation of a parabola that opens up with vertex (h, k)

y = a(x - h)² + k

Vertex (h, k) = (2, -8)

Substitute x = 3 and y = -4 in equation,

-4 = a(3 - 2)² - 8

-4 = a(1) - 8

-4 = a - 8 

a = -4 + 8

a = 4

By applying a = 4 in equation,

y = 4 (x - 2)² - 8

Standard Form:

y = 4 (x - 2)² - 8

Expanding using algebraic identity, we get

y = 4 (x² - 2x(2) + 2²) - 8

y = 4(x² - 4x + 4) - 8

y = 4x² - 16x + 16 - 8

y = 4x² - 16x + 8