FINDING EQUATION OF IMAGE WITH ENLARGEMENT AND REDUCTION

Problem 1 :

Find the equation of the image when

y = 2x is 

i) enlargement with center O (0, 0) and scale factor k = 3

ii) reduced with center O (0, 0) and scale factor k = 1/3

Solution :

y = 2x

i) enlargement with scale factor k = 3

(x, y) --> (kx, ky) --> (3x, 3y)

3y = 2(3x)i

3y = 6x

Dividing by 3, we get

y = 2x

ii)  reduction with scale factor k = 1/3

(x, y) --> ( kx, ky ) --> (x/3, y/3)

Here the value of k is in between 0 and 1.

y/3 = 2(x/3)

y/3 = 2x/3

y = 2x

Problem 2 :

Find the equation of the image when

y = -x + 2 is

i) enlargement with center O (0, 0) and scale factor k = 4

ii) reduced with center O (0, 0) and scale factor k = 2/3

Solution :

i) Let us find the x and y-intercepts to draw the graph of the line.

(2, 0) and (0, 2) are the x and y-intercepts.

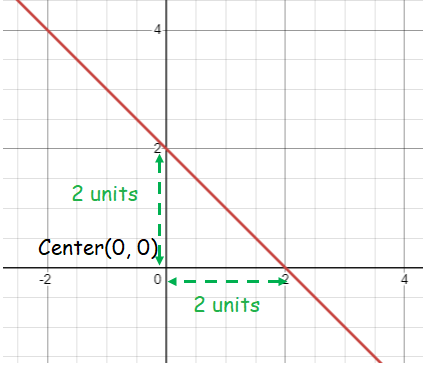
• Distance from center and x-intercept is 2 units. Since we do enlargement with the scale factor of 4, to find the horizontal distance between center and a point on the new line will be 8 units.

• Distance from center and y-intercept is 2 units. Since we do enlargement with the scale factor of 4, to find the vertical distance between center and a point on the new line will be 8 units.

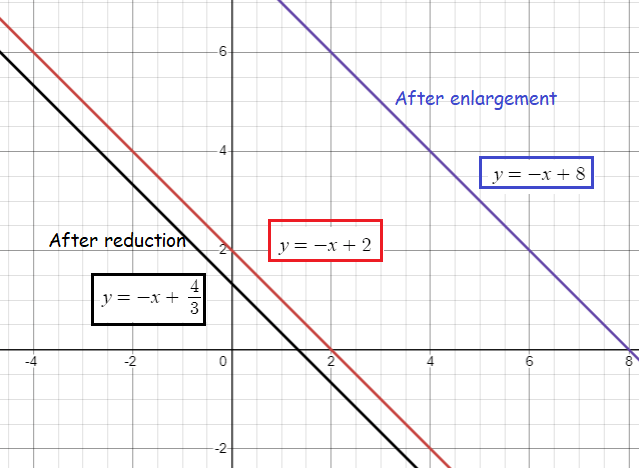
After the enlargement with the scale factor or 4 units :

Slope = 8/8 = 1

It must be a falling line, then m = -1

y-intercept = 8

then,

y = -1x + 8

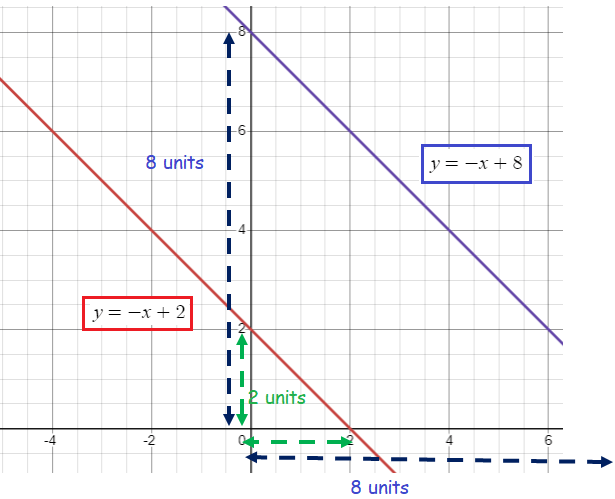
ii) reduced with center O (0, 0) and scale factor k = 2/3

Distance between center and y-intercept of the old line = 2 units.

Since the reduction to be done with 2/3 units, we have to multiply 2 by 2/3. Then we get 4/3. So, the new y-intercept will be 4/3.

There is no change in slope, then 

y = -x + (4/3)

Problem 3 :

Find the equation of the image when

y = 2x + 3 is

i) enlargement with center O (2, 1) and scale factor k = 2

ii) reduced with center O (2, 1) and scale factor k = 1/2

Solution :

i) Let us find the x and y-intercepts to draw the graph of the line.

(-3/2, 0) and (0, 3) are the x and y-intercepts.

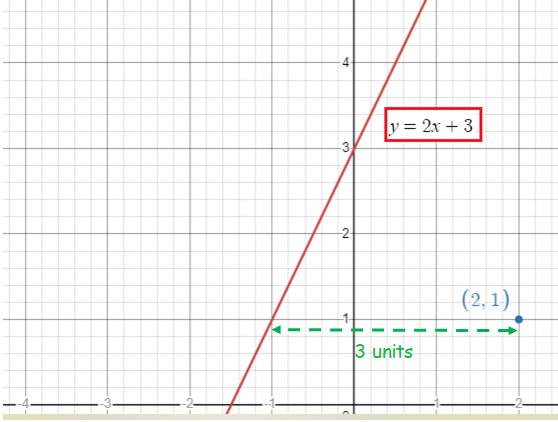
Distance between center and point on the old line :

• The horizontal distance between center (2, 1) and one of the points of the old line is 3 units.
• The vertical distance between center (2, 1) and other points of the old line is 6 units.

Distance between center and point on the old line :

• 3 x 2 ==> 6 units, we trace a point horizontally which is 6 units away from the center (2, 1)
• 6 x 2 ==> 12 units, we trace a point vertically which is 12 units away from the center (2, 1)

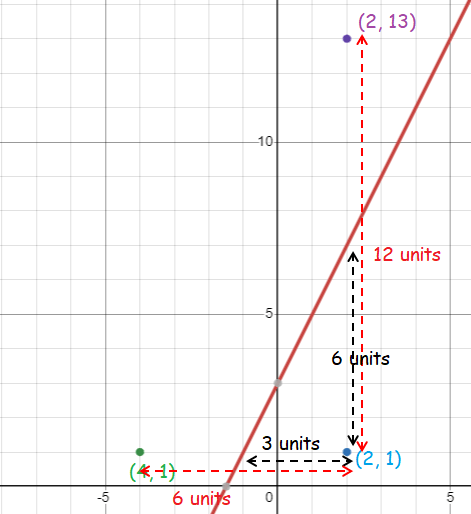
(-4, 1) and (2, 13)

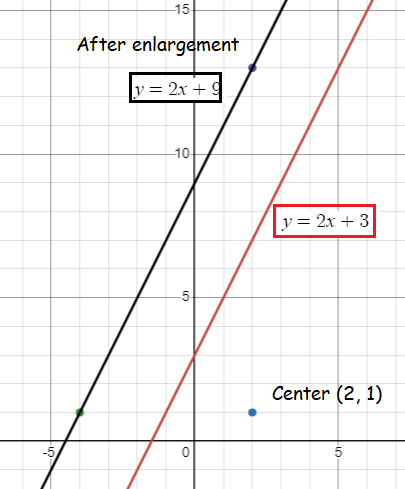
Equation of new line after enlargement :

y = 2x + b

Applying (-4, 1), we get

1 = 2(-4) + b

1 + 8 = b

b = 9

Applying the value of b, we get

y = 2x + 9

ii) reduced with center O (2, 1) and scale factor k = 1/2

Distance between center and point on the old line :

• The horizontal distance between center (2, 1) and one of the points of the old line is 3 units.
• The vertical distance between center (2, 1) and other points of the old line is 6 units.

Distance between center and point on the old line :

• 3 x 1/2 ==> 1.5 units, we trace a point horizontally which is 1.5 units away from the center (2, 1)
• 6 x 1/2 ==> 3 units, we trace a point vertically which is 3 units away from the center (2, 1)

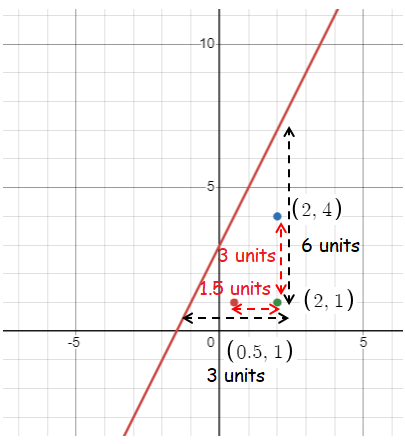
(0.5, 1) and (2, 4)

Equation of new line after enlargement :

y = 2x + b

Applying (2, 4), we get

4 = 2(2) + b

4 - 4 = b

b = 0

Applying the value of b, we get

y = 2x + 0

y = 2x