FINDING DOMAIN AND RANGE OF MODULUS FUNCTION AS INTERVAL NOTATION

Domain :

The set of all possible inputs is known as domain. For absolute value functions all real numbers will be domain.

Because there is no restriction to give inputs. So, for all absolute value functions domain will be  (-∞, ∞).

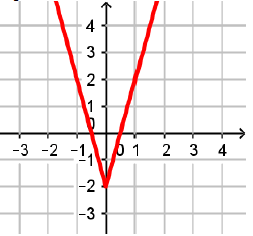
This graph will not go below -2 on y-axis. So, range is

-2 ≤ y ≤∞

Use interval notation to describe the domain and range of the given function.

Problem 1 :

f(x) = |-x|

Solution :

f(x) = |-x|

Domain: (-∞, ∞)

Range: [0, ∞), y ≥ 0

Problem 2 :

f(x) = -|x|

Solution :

f(x) = -|x|

Domain: (-∞, ∞)

Range: (-∞, 0], y ≤ 0

Problem 3 :

f(x) = (1/2)|x|

Solution :

f(x) = (1/2)|x|

Domain: (-∞, ∞)

Range: [0, ∞), y ≥ 0

Problem 4 :

f(x) = -2|x|

Solution :

f(x) = -2|x|

Domain: (-∞, ∞)

Range: (-∞, 0], y ≤ 0

Problem 5 :

f(x) = |x + 4|

Solution :

f(x) = |x + 4|

Domain: (-∞, ∞)

Range: [0, ∞), y ≥ 0

Problem 6 :

f(x) = |x - 2|

Solution :

f(x) = |x - 2|

Domain: (-∞, ∞)

Range: [0, ∞), y ≥ 0

Problem 7 :

f(x) = |x| + 2

Solution :

f(x) = |x| + 2

Domain: (-∞, ∞)

Range: [2, ∞), y ≥ 2

Problem 8 :

f(x) = |x| - 3

Solution :

f(x) = |x| - 3

Domain: (-∞, ∞)

Range: [-3, ∞), y ≥ -3

Problem 9 :

f(x) = |x + 3| + 2

Solution :

f(x) = |x + 3| + 2

Domain: (-∞, ∞)

Range: [2, ∞), y ≥ 2

Problem 10 :

f(x) = |x - 3| - 4

Solution :

f(x) = |x - 3| - 4

Domain: (-∞, ∞)

Range: [-4, ∞), y ≥ -4