FINDING CONSTANT OF PROPORTIONALITY FROM THE TABLE

A unit rate can also be called a constant of proportionality. The constant of proportionality describes the rate at which variables is an equation change.

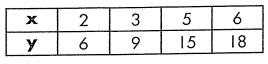
To find constant of proportionality, we may use the formula

k = y/x

k = 6/2 ==> 3

Check if we have the same constant of proportionality for all the values.

k = 9/3 ==> 3

k = 15/5 ==> 3

k = 18/6 ==> 3

Determine the constant of proportionality for each table. Express your answer as y = kx.

Problem 1 :

Every concrete block weighs  _____ kilograms.

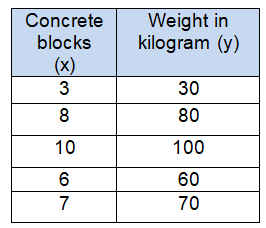
Solution :

Weight 3 blocks = 30 kg

Weight of 1 block = 30/3

= 10 kg

Equation of constant of proportionality :

y = 10x

So, weight of 1 block is 10 kg.

Every concrete block weighs 10 kilograms. 

Problem 2 :

For every can of paint you could paint ___ bird houses.

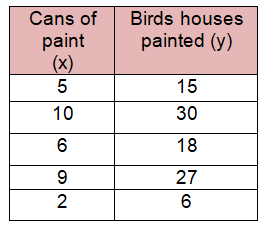
Solution :

Using 5 cans of paint, we are able to paint 15 bird houses.

1 can of paint used to paint = 15/5

= 3 houses.

Equation of constant of proportionality :

y = 3x

For every can of paint you could paint 3 bird houses.

Problem 3 :

For every vote of Faye there were ____ votes of Victor.

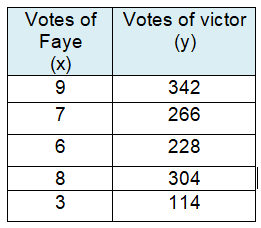
Solution :

If Faye gets 9 votes, then Victor will get 342 votes

If number of votes is 1 for Faye, then 342/9 = 38 votes for Victor.

Equation of constant of proportionality :

y = 38x

For every vote of Faye there were 38 votes of Victor.

Problem 4 :

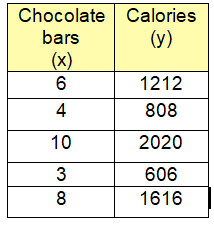
Every single chocolate bars has ____ calories

Solution :

In 6 chocolate bars, there are 1212 calories

In 1 chocolate bar, we have 1212/6 = 202 calories

Equation of constant of proportionality :

y = 202x

So,

Every single chocolate bars has 202 calories.

Problem 5 :

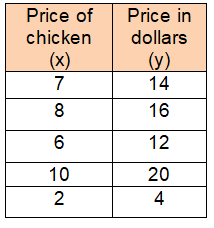
For each piece of chicken it costs _____ dollars.

Solution :

Price of 7 pieces of chicken = $14

Price of 1 piece of chicken = 14/7

= $2

Equation of constant of proportionality :

y = 2x

So,

For each piece of chicken it costs 2 dollars.

Problem 6 :

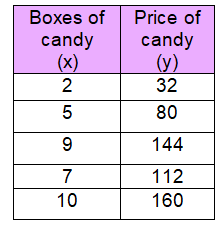
For every box of candy ___ is the price.

Solution :

Cost of 2 boxes of candy = 32

Cost of 1 box of candy = 32/2

= 16

Equation of constant of proportionality :

y = 16x

For every box of candy 16 is the price.

Find the constant of proportionality, then use it to fill the missing values in the table

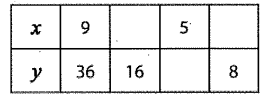
Problem 7 :

Solution :

Constant of proportionality k = y/x

= 36/9

k = 4

The proportional relationship will be the form of y = kx

y = 4x

x = y/4

When y = 16, x = 16/4 ==> 4

When x = 5, y = 4(5) ==> 20

When y = 8, x = 8/4 ==> 2

Problem 8 :

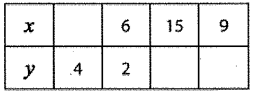
Solution :

Constant of proportionality k = y/x

= 2/6

k = 1/3

The proportional relationship will be the form of y = kx

y = (1/3)x

x = 3y

When y = 4, x = 3(4) ==> 12

When x = 15, y = (1/3)(15) ==> 5

When x = 9, y = (1/3)(9) ==> 3