FINDING COMPOSITION OF FUNCTION FROM GIVEN ORDERED PAIRS

Problem 1 :

Given the function

f = {(-3, 4), (-2, 2), (-1, 0), (0, 1), (1, 3), (2, 4), (3, -1)}

and the function

g = {(-3, -2), (-2, 0), (-1, -4), (0, 0), (1, -3), (2, 1), (3, 2)},

compute the following values.

a) (f ∘ g)(3)

b) (f ∘ f)(0)

c) (g ∘ f)(3)

d) (g ∘ g)(-2)

e) (g ∘ f ∘ g)(0)

f) f(f(f(f(f(1)))))

Solution:

a)

(f ∘ g)(3) = f(g(3))

When 3 is the input, calculating the value of the function g, we get

f(g(3)) = f[2]

When the input is 2, the value of the function f, we get

= 4

b) 

(f ∘ f)(0) = f(f(0))

When 0 is the input, calculating the value of the function f, we get

f(f(0)) = f[1]

When the input is 1, the value of the function f, we get

= 3

c)

(g ∘ f)(3) = g(f(3))

When 3 is the input, calculating the value of the function f, we get

g(f(3)) = g[-1]

When the input is -1, the value of the function g, we get

= -4

d)

(g ∘ g)(-2) = g(g(-2))

When -2 is the input, calculating the value of the function g, we get

g(g(-2)) = g[0]

When the input is 0, the value of the function g, we get

= 0

e)

(g ∘ f ∘ g)(0) = g(f(g(0)))

= g(f(0))

= g(1)

= -3

f)

f(f(f(f(f(1))))) = f(f(f(f(3))))

= f(f(f(-1)))

= f(f(0))

= f(1)

= 3

Problem 2 :

The functions A(x) and B(x) are defined by the tables below.

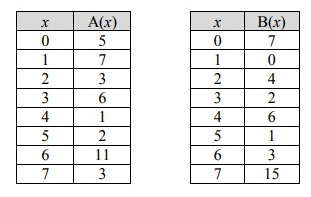
a) A(B(4))

b) B(A(1))

c) B(A(7))

d) A(B(1))

Solution:

a)

A(B(4)) 

When 4 is the input, calculating the value of the function B, we get

A(B(4)) = A[6]

When the input is 6, the value of the function A, we get

= 11

b)

B(A(1)) 

When 1 is the input, calculating the value of the function A, we get

B(A(1)) = B[7]

When the input is 7, the value of the function B, we get

= 15

c)

B(A(7))

When 7 is the input, calculating the value of the function A, we get

B(A(7)) = B[3]

When the input is 3, the value of the function B, we get

= 2

d) 

A(B(1)) 

When 1 is the input, calculating the value of the function B, we get

A(B(1)) = A[0]

When the input is 0, the value of the function A, we get

= 5

Problem 3 :

For f = {(1, 2), (3, 3), (2, 4), (4, 1)} and g = {(1, 3), (3, 4), (2, 2), (4, 1)}, find f ∘ g and g ∘ f if they exist.

Solution:

f[g(1)] = f(3) = 3

f[g(2)] = f(2) = 4

f[g(3)] = f(4) = 1

f[g(4)] = f(1) = 2

f ∘ g = {(1, 3), (2, 4), (3, 1), (4, 2)}

g[f(1)] = g(2) = 2

g[f(2)] = g(4) = 1

g[f(3)] = g(3) = 4

g[f(4)] = g(1) = 3

g ∘ f = {(1, 2), (2, 1), (3, 4), (4, 3)}