FINDING AVERAGE AND INSTANTENOUS RATE OF CHANGE WORKSHEET

Problem 1 :

Use the following table to find the average rate of change on the given interval.

1. [3, 13]

2. 0 ≤ x ≤ 12

3. [3, 4]

Solution

Problem 2 :

The function h(x) is given in the table below. Which of the following choices shows the average rate of change of the function over the interval 2 ≤ x ≤ 6?

Solution

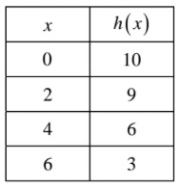
Problem 3 :

Given the functions g(x), f(x) and h(x) shown below.

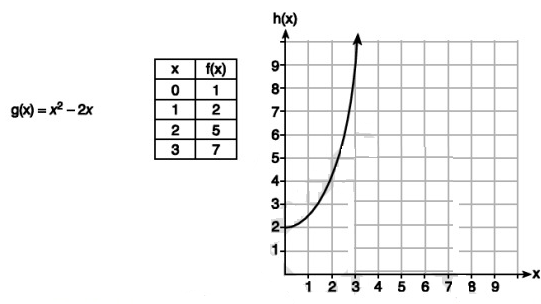
The correct list of functions ordered from greatest to least by average rate of change over the interval 0 ≤ x ≤ 3 is

A. f(x), g(x), h(x)        B. h(x), g(x), f(x)  

C. g(x), f(x), h(x)        D. h(x), f(x), g(x)

Solution

Problem 4 :

Use the table below to estimate the value of d'(120). Indicate units of measures.

Solution

Problem 5 :

Frank is selling lemonade. The function g(t) = (t² + 4)/2 models the number of glasses he sold, g(t), after t hours. What is the average rate of change between hour 2 and hour 6? Show all work.

Solution

Problem 6 :

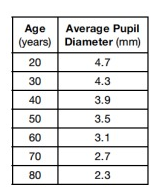
The table shows the average diameter of a person's pupil as a person ages. What is the average rate of change of a person's average pupil diameter from age 30 to 70? Be sure to include units.

Solution

For the following exercises, find the average rate of change of each function on the interval specified.

Problem 1 :

f(x) = x² + 2 on [-1, 2]

Solution

Problem 2 :

f(x) = 4x² - 7 on [1, b]

Solution

Problem 3 :

g(x) = 2x² - 9 on [4, b]

Solution

For each problem, find the average rate of change of the function over the given interval. You may use the provided graph to sketch the function.

Problem 4 :

f(x) = x² - 2x + 1; [0, 1/3]

Solution

Problem 5 :

Solution

Problem 6 :

Solution

Problem 7 :

f(x) = -x² + 1; [-1, -3/4]

Solution