FINDING AREA OF COMPOUND SHAPES

Work out the area of each of these shapes.

Problem 1 :

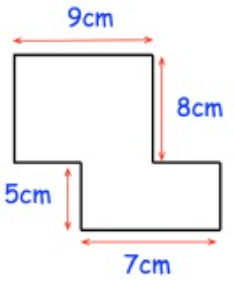
Solution :

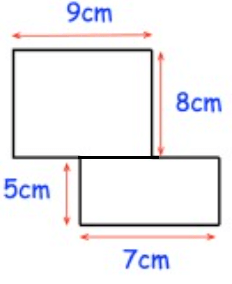
Area of shape given = Area of rectangle + area of rectangle

Area of the rectangle = length x width

= (9 × 8) + (7 × 5)

= 72 + 35

= 107 cm²

Problem 2 :

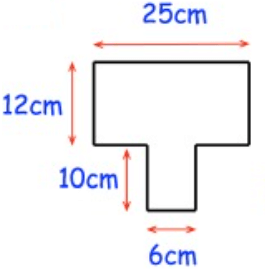
Solution :

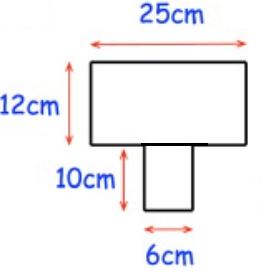
Required area

= Area of large rectangle + area of small rectangle

= (25 × 12) + (6 × 10)

= 300 + 60

= 360 cm²

Problem 3 :

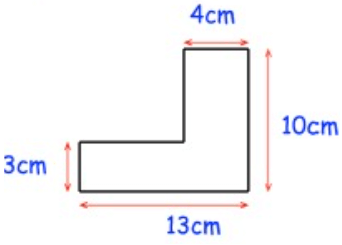
Solution :

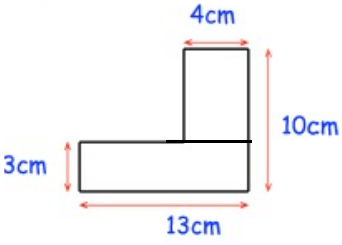
Required area

= Area of rectangle at the bottom + area of rectangle at the top

= (4 × 7) + (13 × 3)

= 28 + 39

= 67 cm²

Problem 4 :

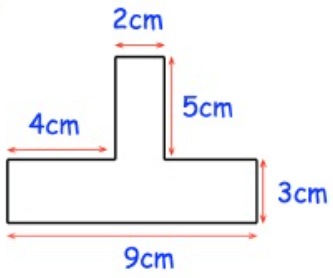
Solution :

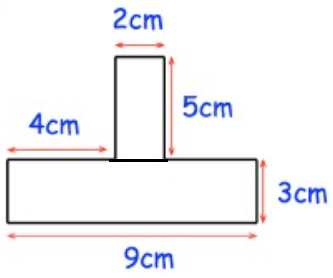
Required area

= Area of rectangle at the bottom + area of rectangle at the top

= (9 × 3) + (2 × 5)

= 27 + 10

= 37 cm²

Problem 5 :

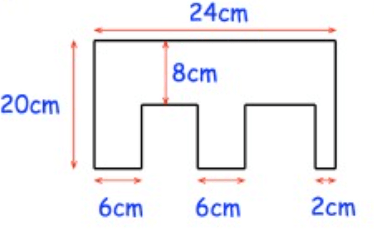
Solution :

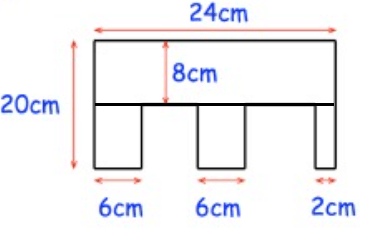
Required area

= Area of large rectangle + area of 3 small rectangles 

= (24 × 8) + (6 × 12) + (6 × 12) + (2 × 12)

= 192 + 72 + 72 + 24

= 360 cm²

Problem 6 :

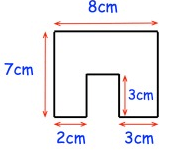
Solution :

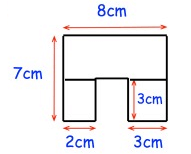
Required area

= Area of large rectangle + area of 2 small rectangles

= (8 × 4) + (2 × 3) + (3 × 3)

= 32 + 6 + 9

= 47 cm²

Problem 7 :

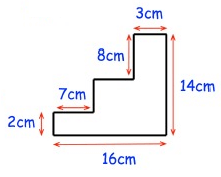
Solution :

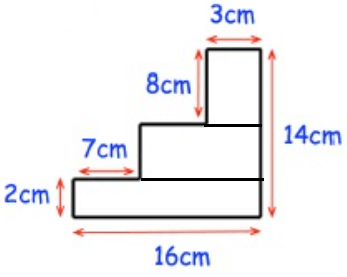
Area of required shape

= Area of rectangle + area of 3 rectangles

= (3 × 8) + (7 × 4) + (16 × 2)

= 24 + 28 + 32

= 84 cm²

Problem 8 :

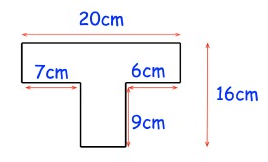
Solution :

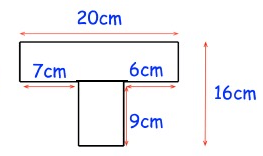
Area of the required shape

= Area of rectangle + area of rectangle

= (20 × 7) + (7 × 9)

= 140 + 63

= 203 cm²

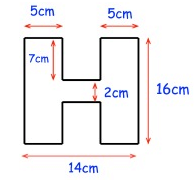
Problem 9 :

Solution :

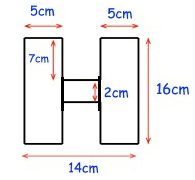
Area of the required shape

= Area of rectangle + area of rectangle + area of rectangle

= (5 × 7) + (4 × 2) + (5 × 7)

= 35 + 8 + 35

= 78 cm²

Problem 10 :

You make a photo prop for a school fair. You cut a 10-inch square out of a parallelogram-shaped piece of wood. What is the area of the photo prop? 

Solution :

Area of the photo prop = Area of parallelogram - area of square

1 ft = 12 inches

8 ft = 8 x 12

= 96 inches

4 ft = 4 x 12

= 48 inches

= 96 x 48 - 10 x 10

= 4608 - 100

= 4508 square inches

Problem 11 :

You can use a trapezoid to approximate the shape of Scott County, Virginia. The population is about 23,200. About how many people are there per square mile?

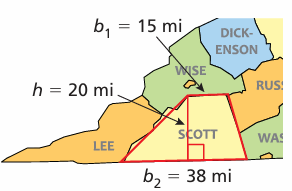
Solution :

Are of trapezium = 1/2 x base x sum of lengths of parallel sides

h = 20 miles, b₁ = 15 miles and b₂ = 38 miles

= (1/2) x 20 x (15 + 38)

= 10 x 53

= 530 square miles

Total population = 23200

Total area = 530 miles

Number of people per square mile = 23200/530

= 43.77

Approximately 44 people per square mile.

Problem 12 :

Light shines through a window. What is the area of the trapezoid-shaped region created by the light?

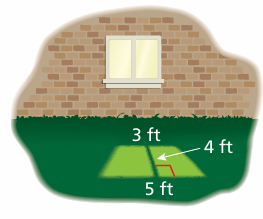
Solution :

The field is in the shape of trapezium,

height = 4 ft, lengths of bases = 3 ft and 5 ft.

= (1/2) x 4 x (3 + 5)

= 2 x 8

= 16 square ft

Problem 13 :

The triangle and the trapezoid share a 15-inch base and a height of 10 inches.

a. The area of the trapezoid is less than twice the area of the triangle. Find the values of x. Explain your reasoning.

b. Can the area of the trapezoid be exactly twice the area of the triangle? Explain your reasoning.

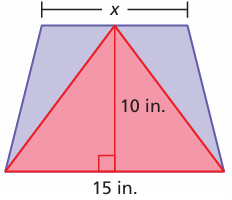
Solution :

Area of trianlge = 1/2 x base x height

= (1/2) x 15 x 10

= 75 square units

Area of trapezium = (1/2) x 10 x (15 + x)

= 5(15 + x)

a) 

Given that,

area of trapezum = 2(area of triangle)

5(15 + x) = 2(75)

75 + 5x = 150

5x = 150 - 75

5x = 75

x = 75/5

x = 15

b) Applying x = 15,

= 5(15+15)

= 5(30)

= 150 square units

Yes area of trapezium is twice the area of triangle.

Problem 14 :

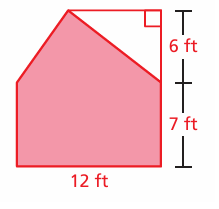
Solution :

At the top, we have triangle and at the bottom we have rectangle.

Area of triangle = (1/2) x 12 x 6

= 36 square ft

Area of rectangle = 12 x 7

= 84 square ft

Total area = 36 + 84

= 120 square ft

Problem 15 :

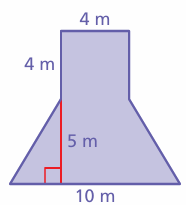
Solution :

Area of the shape given = Area of square + area of trapezium

= 4² + (1/2) x 5 x (4 + 10)

= 16 + (1/2) x 5 x 14

= 16 + 35

= 51 square meter

Problem 16 :

Solution :

Area of the shape given = Area of rectangle - area of triangle + area of trapezium

= (14 + 4) x 4 - 1/2 x 4 x 4 + 1/2 x 4 x (14 + 18)

= 18 x 4 - 8 + 2 x 32

= 72 - 8 + 64

= 128 square inches