FINDING AREA AND PERIMETER OF REGULAR POLYGONS

Find the perimeter area of each regular polygon. Leave your answer in simplest form.

Example 1 :

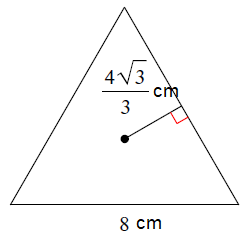
Solution :

The given triangle must be a equilateral triangle, because it is regular polygon.

Perimeter of equilateral triangle = 3 x side 

= 3(8)

Perimeter = 24 cm

Example 2 :

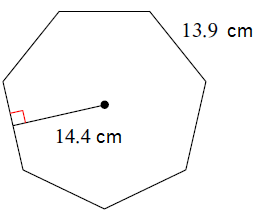
Solution :

Number of sides = 7

Perimeter of the shape = 7 x 13.9

= 97.3

Perimeter = 97.3 cm

Length of apothem = 14.4 cm

Example 3 :

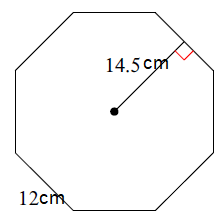
Solution :

Number of sides = 8

Perimeter of the shape = 8 x 12

= 96 cm

Perimeter = 96 cm

Length of apothem = 14.5 cm

Example 4 :

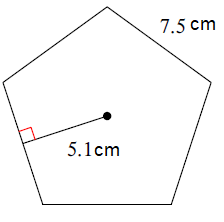
Solution :

Number of sides = 5

Perimeter of the shape = 5 x 7.5

= 37.5 cm

Perimeter = 37.5 cm

Length of apothem = 5.1 cm

Example 5 :

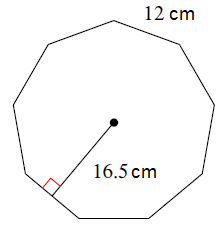
Solution :

Number of sides = 9

Perimeter of the shape = 9 x 12

= 108 cm

Perimeter = 108 cm

Length of apothem = 16.5 cm

Example 6 :

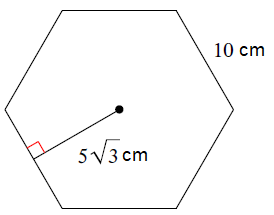
Solution :

Number of sides = 6

Perimeter of the shape = 6 x 10

= 60 cm

Perimeter = 60 cm

Length of apothem = 5√3 cm

Example 7 :

You are decorating the top of a table by covering it with small ceramic tiles. The tabletop is a regular octagon with 15-inch sides and a radius of about 19.6 inches. What is the area you are covering?

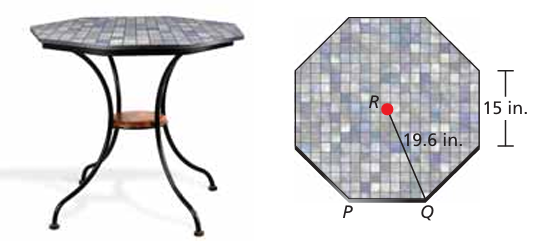
Solution :

Step 1 :

Find the perimeter P of the tabletop. An octagon has 8 sides,

so, P = 8(15) = 120 inches.

Step 2 :

Find the apothem a.

The apothem is height RS of △PQR. Because △PQR is isosceles, altitude RS bisects QP.

So, QS = (1/2)  (QP) = (1/2)  (15) = 7.5 inches.

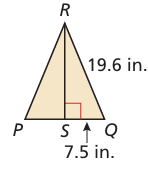
To fi nd RS, use the Pythagorean Theorem (Theorem 9.1) for △RQS.

a = RS = √19.6² − 7.5²

= √327.91

≈ 18.108

Step 3 :

Find the area A of the tabletop.

A = (1/2)  aP

= (1/2)   (√327.91 ) (120)

≈ 1086.5

The area you are covering with tiles is about 1086.5 square inches.

Example 8 :

Use the diagram.

a) Identify the center of polygon JKLMN.

b) Identify a central angle of polygon JKLMN.

c) What is the radius of polygon JKLMN?

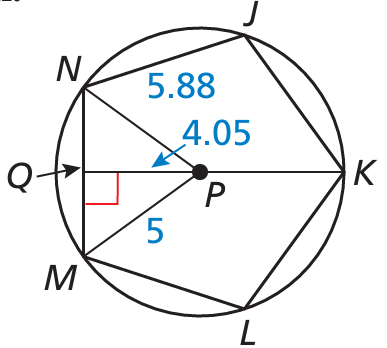
Solution :

a)  NM = 5.88

QN = (1/2) NM

= (1/2) x 5.88

= 2.94

b) The centeral angle = 360

= (1/5) of 360

= 72

= 360 - 72

c) Radius = 5

Example 9 :

Find the area of the shaded region.

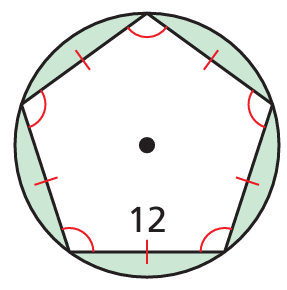
Solution :

Area of shaded region = area of circle - area of pentagon

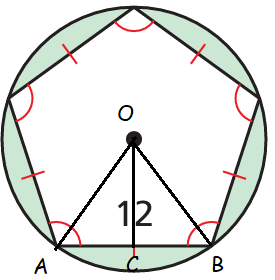
Angle created by the triangle with center = 360/5

= 72

Considering the triangle OCB,

<OCB = 90, <CBO = 36 and <COB = 36

BC = CO = 6

Area of pentagon = (1/2) x perimeter x apothem

= (1/2) x 5(12) x 6

= (1/2) x 60 x 6

= 180 square units

Using Pythagorean theorm in triangle OCB :

OB² = OC² + BC²

OB² = 6² + 6²

= 36 + 36

= 72

OB = √72

= 8.48

Area of shaded region = πr² - 180

= 3.14 (√72)² - 180

= 226.08 - 180

= 46.08 square units

Example 10 :

The perimeter of a regular nonagon, or 9-gon, is 18 inches. Is this enough information to find the area? If so, find the area and explain your reasoning. If not, explain why not.

Solution :

Perimeter of regular polygon = 18 inches

Let a be the side length of nanogon

Number of sides of a nanogon = 9

9a = 18

a = 2 inches

To find area of polygon, we will use the formula 1/2 x perimeter x apothem.

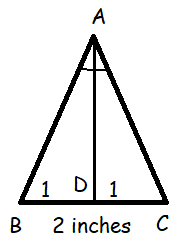
<BAC = 360/9

= 40 degree

<DAC = 20 degree

<BCA = 40

tan 40 = AD/DC

0.839 = AD/1

AD = 0.839

Area of nanogon = (1/2) x AD x 18

= (1/2) x 0.839 x 18

= 9 x 0.839

= 7.551 square inches