FINDING HCF AND LCM USING LADDER METHOD

Find the HCF of LCM of following numbers using prime factorization method :

Problem 1 :

9, 12

Solution :

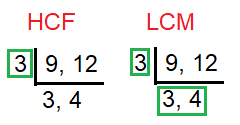
HCF of (9, 12) = 3

LCM of (9, 12) = 4 x 3² ==> 36 

Problem 2 :

8, 16

Solution :

8, 16

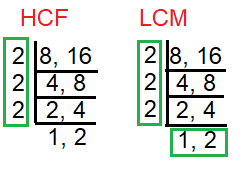
HCF of (8, 16) = 2³ ==> 8

LCM of (8, 16) = 2⁴ ==> 16

Problem 3 :

18, 42

Solution :

18, 42

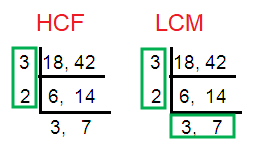
HCF of (18, 42) = 3 × 2 ==> 6

LCM of (18, 42) = 3² × 2 x 7 ==> 126

Problem 4 :     

14, 42

Solution :

14, 42

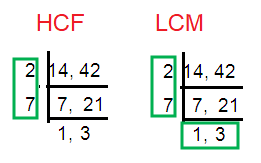
HCF of (14, 42) = 2 × 7 ==> 14

LCM of (14, 42) = 2 × 3 x 7 ==> 42

Problem 5 :

18, 30

Solution :

18, 30

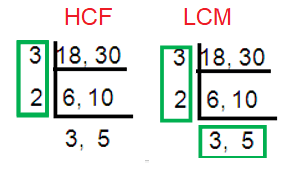
HCF of (18, 30) =  3 × 2 ==> 6

LCM of (18, 30) =  3² × 2 x 5 ==> 90

Problem 6 :

24, 32

Solution :

24, 32

HCF of (24, 32) = 2³ ==> 8

LCM of (24, 32) = 2⁵ x 3 ==> 96

Problem 7 :

12, 36

Solution :

12, 36

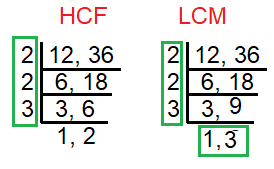
HCF of (12, 36) = 3 × 2² ==> 12

LCM of (12, 36) = 3² × 2²  ==> 36

Problem 8 :

15, 33

Solution :

15, 33

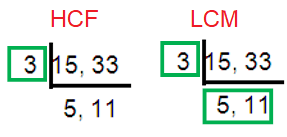
HCF of (15, 33) = 3

LCM of (15, 33) = 3 x 11 x 5 ==> 165

Problem 9 :

72, 96

Solution :

72, 96 

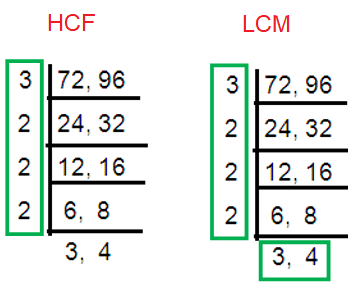
HCF of (72, 96) = 3 × 2³ ==> 24

LCM of (72, 96) = 3² × 2⁵ ==> 288

Problem 10 :

108, 144

Solution :

108, 144

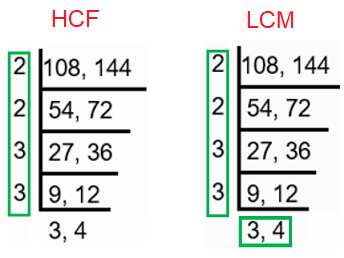
HCF of (108, 144) = 2² x 3² ==> 36

LCM of (108, 144) = 2⁴ x 3³ ==>  432

Problem 11 :

78, 130

Solution :

78, 130

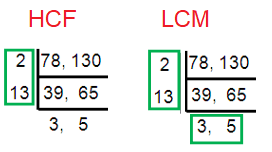
78 = 2 × 3 x 13

130 = 2 × 5 x 13

HCF of (78, 130) ==> 26

LCM of (78, 130) = 2 x 5 x 3 x13 ==> 390

Problem 12 :

LCM of co-prime numbers is the ________ of the numbers.

Solution :

If two or more numbers which are having its HCF as 1, then it is called co-primes. Let us conside two co-prime numbers, 3 and 4. Its least common multiple is 12.

Problem 13 :

Find the least length of a rope which can be cut into whole number of pieces of lengths 45 cm, 75 cm and 81cm.

Solution :

LCM of 45, 75 and 81

= 3 x 5 x 3 x 5 x 9

= 2025

So, the least lenght of the rope is 2025 cm.

Problem 14 :

Find the smallest number which when increased by 20 is exactly divisible by 90 and 144.

Solution :

If the number is divisible by 90 and 144, then it must be the multiple of these two numbers.

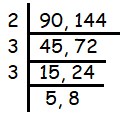
LCM = 2 x 3 x 3 x 5 x 8

= 720

The least common multiple of 90 and 144 is 720, it is 20 increased from 700. So, the required number is 700.

Problem 15 :

LCM of co-prime numbers is the ________ of the numbers

a) sum      b) difference      c) product        d) quotient 2

Solution :

Least common multiple of two co-prime numbers is its product.

Problem 16 :

The HCF of two numbers is 24. The number which can be their LCM is ______.

a) 84        b) 120     c) 128      d) 148

Solution :

Since HCF of two numbers is 24, the two numbers must be a multiple of 24. Its least common multiple be the multiple of 24.

Option a :

84 is not divisible by 24.

Option b :

120 is divisble by 24.

So, its least common multiple is 120.

Problem 17 :

LCM of two numbers is 12 times their HCF. The product of the numbers is 3072. Find their HCF and LCM.

Solution :

Let a and be those two numbers.

LCM of a and b = 12 x HCF

The product of two numbers = 3072

a x b = 3072

Product of two numbers = product of its HCF and LCM

12a x 12b = HCF x 12 x HCF

(12 x 12 x 3072)/12 = (HCF)²

(HCF)² = 3072 x 12

HCF = 192

LCM of those two numbers =  12 x 192

= 2304

Problem 18 :

If the ratio of two numbers is 4:5 and their HCF is 4, then find their LCM.

Solution :

Let 4x and 5x be those two numbers.

HCF = 4

For 16 and 20, its HCF is 4. Then the required numbers are 16 and 20.

Problem 19 :

The LCM of two numbers is 12 times their HCF. The sum of the HCF and LCM is 403. If one number is 93, then find the other.

Solution :

Let a be the other number.

One number is 93

LCM of two numbers = 12 HCF

Sum of HCF and LCM = 403

x + 12x = 403

13x = 403

x = 403/13

x = 31

Its HCF is 31 and LCM is 12(31) is 372.

93 x a = 31 x 372

a = (31 x 372) / 93

= 124

So, the required number is 124.