FIND ZEROES OF QUADRATIC POLYNOMIAL

Find the zeroes of quadratic polynomial given below.

Problem 1 :

y = (x - 4)² - 25

Solution :

y= (x - 4)² - 25

(x - 4)² = 25

x - 4 = √25

x - 4 = ±5

So, the zeroes are 9 and -1.

Problem 2 :

y = 2x² - 9x - 5

Solution :

y = 2x² - 9x - 5

To find zeroes, put y = 0

0 = 2x² - 10x + 1x - 5

By using grouping method.

0 = 2x(x - 5) + 1(x - 5)

0 = (2x + 1) (x - 5)

Equating each factor to 0, we get

So, the zeroes are -1/2 and 5.

Problem 3 :

f(x) = 3x² + 5x - 12

Solution :

To find zeroes, Put f(x) = 0

3x² + 5x - 12 = 0

3x² + 9x - 4x - 12 = 0

3x(x + 3) - 4(x + 3) = 0

(3x - 4)(x + 3) = 0

Equating each factor to 0.

So, the zeroes are -3 and 4/3.

Problem 4 :

f(x) = (-1/2) (x + 3)² + 8

Solution :

To find zeroes, Put f(x) = 0

 (-1/2) (x + 3)² + 8 = 0

(-1/2)(x + 3)² = -8

Multiplying by -2 on both sides, we get

(x + 3)² = -8 (-2)

(x + 3)² = 16

x + 3 = √16

x + 3 = ±4

Decomposing into two branches, we get

So, the zeroes are -7 and 1.

Problem 5 :

f(x) = x² - 24x + 144

Solution :

To find zeroes, Put f(x) = 0

x² - 24x + 144 = 0

x² - 12x - 12x + 144 = 0

x(x - 12) - 12(x - 12) = 0

(x - 12) (x - 12) = 0

Equating each factor to 0, we get

x = 12.

Problem 6 :

f(x) = 9x² - 81

Solution :

To find zeroes, Put f(x) = 0

9x² - 81 = 0

9x² = 81

Dividing by 9 on both sides.

x² = 9

x = √9

x = ±3

So, the zeroes are -3 and 3.

Problem 7 :

f(x) = x² - x - 20

Solution :

To find zeroes, Put f(x) = 0

x² - x - 20 = 0

x² - 5x + 4x - 20 = 0

By grouping

x(x - 5) + 4(x - 5) = 0

(x + 4) (x - 5) = 0

Equating each factor to zero, we get

x + 4 = 0 and x - 5 = 0

x = -4 and x = 5

So, the zeroes are -4 and 5.

Problem 8 :

A soccer player kicks a ball downfield. The height of the ball increases until it reaches a maximum height of 8 yards, 20 yards away from the player. A second kick is modeled by

y = x(0.4 − 0.008x)

Which kick travels farther before hitting the ground? Which kick travels higher?

Solution : 

Maximum value by the first kick :

Height reached by the ball in the first kick is 8 yards and reaches the horizontal distance of 20 yards from the starting position. 

Maximum value by the second kick :

y = x(0.4 − 0.008x)

y = 0.4x − 0.008x²

y = - 0.008x² + 0.4x

a = -0.008 and b = 0.4

x = -0.4/2(-0.008)

= 0.4/0.016

= 25

Finding x-intercepts :

y = x(0.4 − 0.008x)

y = 0

 x(0.4 − 0.008x) = 0

x = 0 and -0.008x = -0.4

x = 0.4/0.008

x = 50

Horizontal distance covered by the second kick is 50 yards.

• 8 yards < 25 yards, the second kick reaches the maximum height.
• 20 yards < 50 yards, the second kick has covered the maximum length.

Problem 9 :

Graph the function. Label the x-intercept(s), vertex, and axis of symmetry.

a)  y = (x + 3)(x − 3)

b)  y = (x + 1)(x − 3)

Solution :

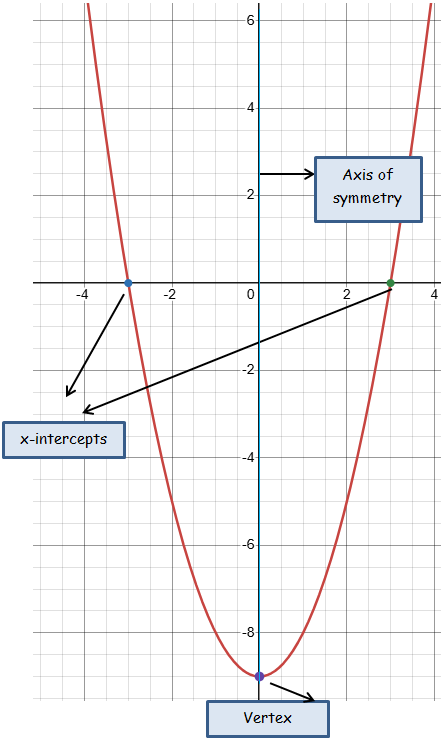
a) y = (x + 3)(x − 3)

Finding x-intercepts :

Put y = 0

(x + 3)(x - 3) = 0

x = -3 and x = 3

Finding vertex :

y = x² - 9

y = (x - 0)² - 9

Vertex (h, k) ==> (0, -9)

Finding axis of symmetry :

Equation of axis of symmtery x = 0

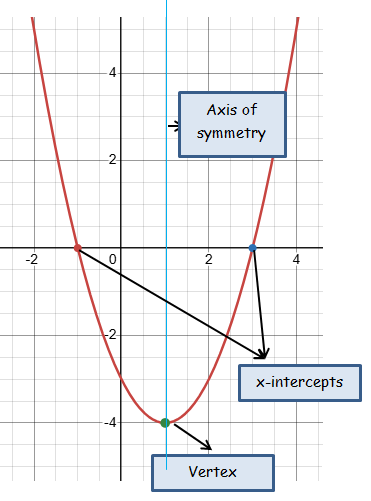
b)  y = (x + 1)(x − 3)

Finding x-intercepts :

Put y = 0

(x + 1)(x - 3) = 0

x = -1 and x = 3

Finding vertex :

y = x² - 3x + 1x - 3

y = x² - 2x - 3

y = x² - 2x + 1² - 1² - 3

y = (x - 1)² - 1 - 3

y = (x - 1)² - 4

Vertex (h, k) ==> (1, -4)

Finding axis of symmetry :

Equation of axis of symmtery x = 1

Problem 10 :

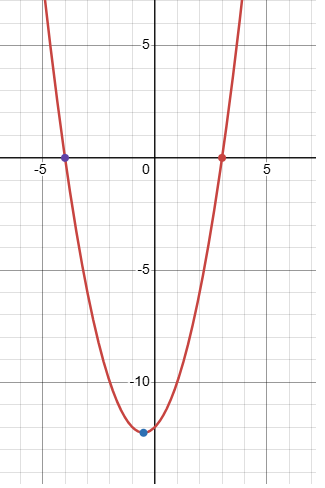
Write the quadratic function f(x) = x² + x − 12 in intercept form. Graph the function. Label the x-intercepts, y-intercept, vertex, and axis of symmetry.

Solution :

f(x) = x² + x − 12

= x² + 4x - 3x − 12

= x(x + 4) - 3(x + 4)

y = (x - 3)(x + 4)

Finding x-intercepts :

Put y = 0

0 = (x - 3)(x + 4)

x = 3 and x = -4

Finding y-intercepts :

Put x = 0

y = 0² + 0 − 12

y = -12

Finding vertex :

f(x) = x² + x − 12

= (x + 1/2)² - (1/2)² − 12

= (x + 1/2)² - (1/4) − 12

= (x + 1/2)² - (49/4)

Vertex (h, k) ==> (-1/2, -49/4)

Axis of symmetry :

x = -1/2