FIND VERTEX OF ABSOLUTE VALUE FUNCTION

Any absolute value function will be in the form 

y = a|x - h| + k

Here (h, k) is vertex.

Vertex can be minimum or maximum point.

• If the curve opens up, then it will have minimum point at vertex.
• If the curve opens down, then it will have maximum point at vertex.

Here a represents slope,

• If a is positive, then the curve will open up.
• If a is negative, then the curve will open down.

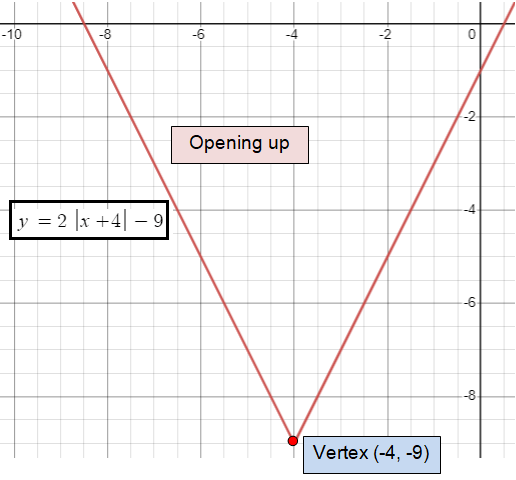
Find the vertex of absolute value function given below and find the direction of opening.

Problem 1 :

y = 1/4│x + 4│- 9

Solution :

y = 1/4│x + 4│- 9

Comparing the given function with

y = a │x - h│+ k

y = 1/4 │x - (-4)│- 9

Vertex (h, k) = (-4, -9)

a = 1/4

It is positive, so it will open up.

Problem 2 :

y = -2│x + 1│+ 6

Solution :

y = -2│x + 1│+ 6

y = a │x - h│+ k

y = -2 │x - (-1)│+ 6

Vertex (h, k) = (-1, 6)

a = -2

It is negative, so it opens down.

Problem 3 :

y = 4│x - 3│

Solution :

y = 4│x - 3│

Compare with

y = a │x - h│+ k

y = 4 │x - 3│+ 0

Vertex (h, k) = (3, 0)

a = 4

It is positive, so it will open up.

Problem 4 :

y = -1/2│x│+ 3

Solution :

y = -1/2│x│+ 3

Compare with 

y = a │x - h│+ k

y = -1/2 │x - 0│+ 3

Vertex (h, k) = (0, 3)

a = -1/2

It is negative, so it will open down.

Problem 5 :

y = -5│x - 8│- 5

Solution :

y = -5│x - 8│- 5

Vertex (h, k) = (8, -5)

a = -5

It is negative, so it will open down. 

Problem 6 :

The number of boats B a boat dealer sells in each month of the year from March to December can be modeled by the function 

B = -15|t - 5| + 120

where t is the time in months and t = 1 represents January.

a) Complete the table of values and then graph the function.

b) What is the maximum number of sales in one month ?

In what month is the maximum reached ?

c) What is the minimum number of sales in one month ? In what month is the minimum reached ?

Solution :

B = -15|t - 5| + 120

a)

b) From the given function, it is clear that the absolute value function is opening down. The maximum value will be at vertex.

B = -15|t - 5| + 120

h = 5 and k = 120

Maximum sales = 120 boats

At the month of may, the maximum sales has reached.

c)  From the table, the minimum is (12, 15), so the minimum number of boats sold is 15 and in the month of December.