FIND VALUES OF TRIGONOEMTERIC FUNTIONS USING UNIT CIRCLE

What is unit circle ?

The unit circle is a circle with radius one.

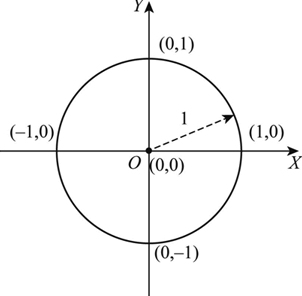
To find values of trigonometric functions using unit circle, we have to follow the given steps.

i) Identify the angle that lies in which quadrant.

ii) Find the reference angle if it is necessary, using the reference angle draw the triangle.

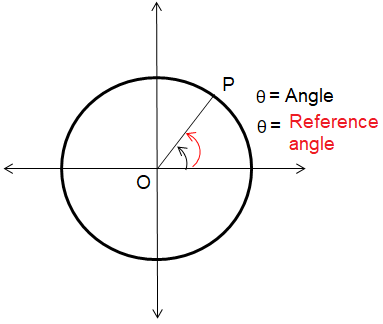	θ lies in 1st quadrant
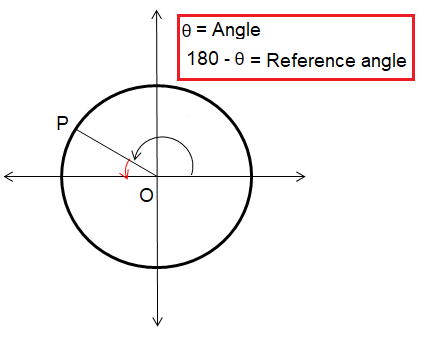	If θ lies in 2 nd quadrant
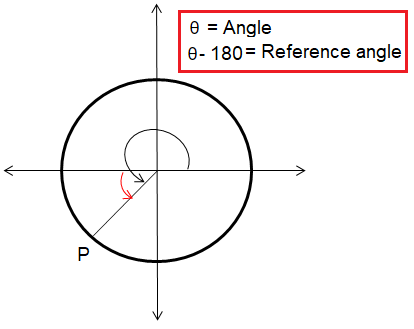	If θ lies in the third quadrant
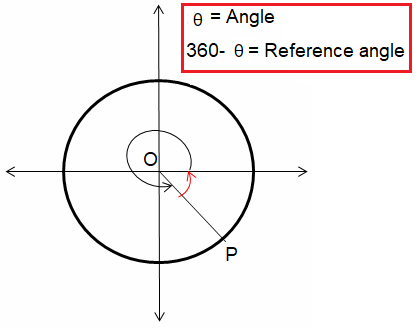	If θ lies in the fourth quadrant

iii)  Point p can be written in the form of (cos θ, sin θ)

iv) Using the concept of special right triangles, we can find values of trigonometric functions.

Solve the following problems using unit circle.

Example 1 :

cos (π/4)

Solution :

θ = π/4

0 ≤ θ ≤ π/2

θ lies in the first quadrant.

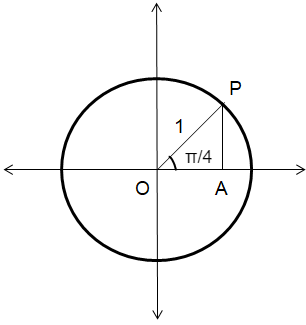
Triangle OPA is 45-45-90 special right triangle.

∠OPA = 45, ∠OAP = 90, ∠POA = 45

OP = √2 OA

1 = √2 OA

OA = 1/√2

OA = √2/2

cos θ = Adjacent side / Hypotenuse

cos (π/4) = OA/OP

 = √2/2/1

cos (π/4) = √2/2

Example 2 :

cos 135

Solution :

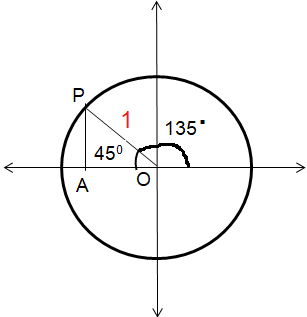
Triangle OPA is 45-45-90 special right triangle.

∠OPA = 45, ∠OAP = 90, ∠POA = 45

OP = √2 OA

1 = √2 OA

OA = 1/√2

OA = √2/2

Point P would be in the form of p(-x, y) ==> p(-OA, AP)

cos θ = Adjacent side / Hypotenuse

cos 135 = OA/OP

 = -√2/2/1

cos 135 = -√2/2

Example 3 :

sin 5π/6

Solution :

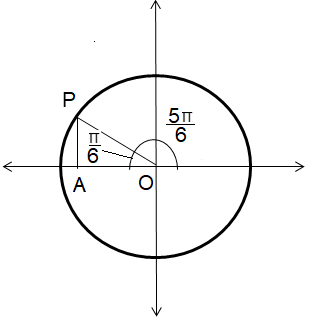
Triangle OPA is 45-45-90 special right triangle.

∠OPA = 60, ∠OAP = 90, ∠POA = 30

OP = 2 PA

1 = 2 PA

PA = 1/2

Point P would be in the form of p(-x, y) ==> p(-OA, AP)

sin θ = Opposite side / Hypotenuse

sin (5π/6) = PA/OP

 = 1/2

sin (5π/6) = 1/2

Example 4 :

sin (-π/3)

Solution :

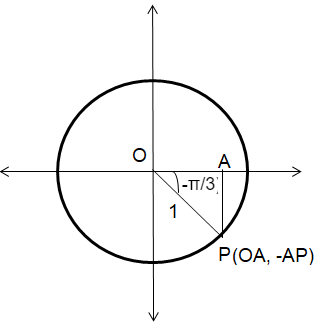
Triangle OPA is 45-45-90 special right triangle.

∠OPA = 30, ∠OAP = 90, ∠POA = 60

Point P would be in the form of p(x, -y) ==> p(OA, -AP)

sin θ = Opposite side / Hypotenuse

sin (5π/6) = PA/OP

sin (-π/3) = -√3/2/1

sin (-π/3) = -√3/2

Example 5 :

tan 135

Solution :

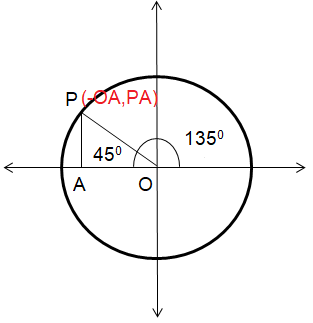
Triangle OPA is 45-45-90 special right triangle.

∠OPA = 45, ∠OAP = 90, ∠POA = 45

OP = √2 OA

1 = √2 OA

OA = 1/√2

OA = √2/2 = PA

Point P would be in the form of p(-x, y) ==> p(-OA, AP)

tan θ = Opposite side / Adjacent side

= -OA/OP

 = -(√2/2) / (√2/2)

tan 135 = -1

Example 6 :

cos (-120)

Solution :

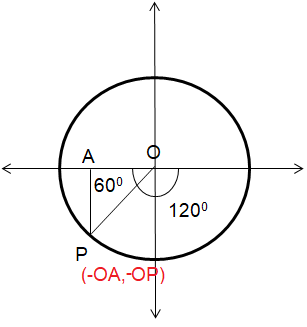
Triangle OPA is 30-60-90 special right triangle.

∠OPA = 30, ∠OAP = 90, ∠POA = 60

OP = 2 OA

1 = 2 OA

OA = 1/2

Point P would be in the form of p(-x, y) ==> p(-OA, -AP)

cos θ = Adjacent side/hypotenuse

cos (-120) = OA/OP

= (-1/2)/1

cos (-120) = -1/2

Example 7 :

tan (3π/2)

Solution :

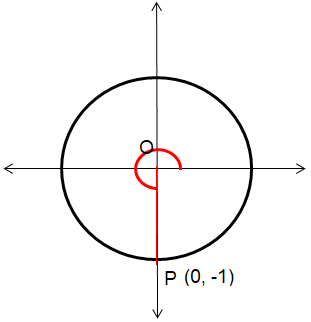
tan 3π/2 = sin 3π/2 / cos 3π/2

= -1/0

= undefined

Example 8 :

sin (-π/4)

Solution :

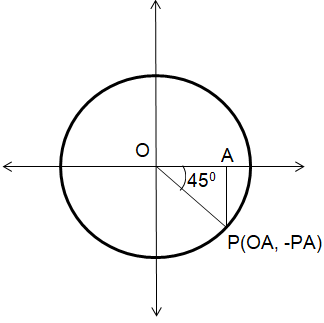
Triangle OPA is 45-45-90 special right triangle.

∠OPA = 45, ∠OAP = 90, ∠POA = 45

OP = √2 OA

1 = √2 OA

OA = 1/√2 = AP

Point P would be in the form of p(x, -y) ==> p(OA, -AP)

sin θ = Opposite side/hypotenuse 

sin (-π/4) = OA/OP

 = (-1/√2) / 1

= -1/√2