FIND UNKNOWN IN PYTHAGOREAN TRIPLES

Find k given that the following are Pythagorean triples :

Problem 1 :

{9, k, 15}

Solution :

{9, k, 15}

9² + k² = (15)²

k² = (15)² - 9²

k² = 225 – 81

k² = 144

Take square root of both sides, we get

k =√144

k = 12

So, {9, k, 15} is a Pythagorean triple.

Problem 2 :

{8, 15, k}

Solution :

{8, 15, k}

8² +(15)² = k²

64 + 225 = k²

289 = k²

Take square root of both sides, we get

k =√289

k = 17

Problem 3 :

{k, 24, 26}

Solution :

{k, 24, 26}

k² + (24)² = (26)²

k² = (26)² – (24)²

k² = 676 – 576

k² = 100

Take square root of both sides, we get

k =√100

k = 10

So, {k, 24, 26} is a Pythagorean triple.

Problem 4 :

{11, k, 61}

Solution :

{11, k, 61}

(11)² + k² = (61)²

k² = (61)² – (11)²

k² = 3721 – 121

k² = 3600

Take square root of both sides, we get

k =√3600

k = 60

How to Check If the Given Numbers are Pythagorean Triples

Check if the following sets of numbers form Pythagorean triples?

Problem 5 :

{3, 7, 9}

Solution :

{3, 7, 9}

3² + 7² = 9²

9 + 49 = 81

58 = 81

So, {3, 7, 9} is not a Pythagorean triple.

Problem 6 :

{14, 48, 50}

Solution :

{14, 48, 50}

(14)² + (48)² = (50)²

196 + 2304 = 2500

2500 = 2500

So, {3, 7, 9} is a Pythagorean triple.

Problem 7 :

{7.5, 10, 12.5}

Solution :

{7.5, 10, 12.5}

(7.5)² + (10)² = (12.5)²

56.25 + 100 = 156.25

156.25 = 156.25

So, {7.5, 10, 12.5} is a Pythagorean triple.

Problem 8 :

{5, 12, 13}

Solution :

{5, 12, 13}

5² + (12)² = (13)²

25 + 144 = 169

169 = 169

So, {5, 12, 13} is a Pythagorean triple.

Problem 9 :

{7, 24, 25}

Solution :

{7, 24, 25}

7² + (24)² = (25)²

49 + 576 = 625

625 = 625

So, {7, 24, 25} is a Pythagorean triple.

Problem 10 :

{8, 15, 17}

Solution :

{8, 15, 17}

8² + (15)² = (17)²

64 + 225 = 289

289 = 289

So, {8, 15, 17} is a Pythagorean triple. 

Problem 11 :

Verify that segments with lengths of 4.3 feet, 5.2 feet, and 6.1 feet form a triangle. Is the triangle acute, right, or obtuse?

Solution :

Let a, b and c be the three sides of the triangle. Let c be the longest side.

a = 4.3 feet, b = 5.2 feet and c = 6.1 feet

If it is right triangle, the measures should satisfy the Pythagorean theorem.

6.1² = 4.3² + 5.2²

37.21 = 18.49 + 27.04

37.21 = 45.53

Which is not true, inorder to make the statement true, we may use the < sign. Then it must be a acute triangle.

Problem 12 :

You are playing capture the flag. You are 50 yards north and 20 yards east of your team’s base. The other team’s base is 80 yards north and 60 yards east of your base. How far are you from the other team’s base?

Solution :

Step 1: Draw the situation in a coordinate plane. Let the origin represent your team’s base. From the descriptions, you are at (20, 50) and the other team’s base is at (60, 80).

Step 2: Draw a right triangle with a hypotenuse that represents the distance between you and the other team’s base. The lengths of the legs are 30 yards and 40 yards.

Step 3: Use the Pythagorean Theorem to find the length of the hypotenuse.

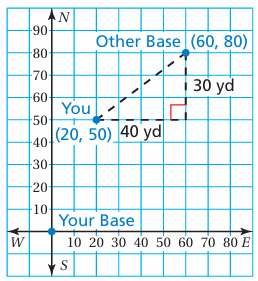
30² + 40² = c²

900 + 1600 = c²

c² = 2500

c = √2500

c = 50

Problem 13 :

Describe and correct the error in finding the missing length of the triangle.

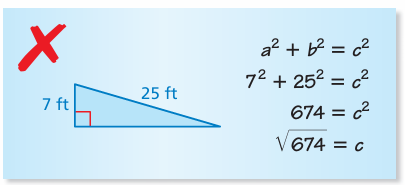
Solution :

Using Pythagorean theorem, the measure of hypotenuse is 25 ft. 

c = 25 ft, a = 7 ft and b = ?

7² + b² = 25²

49 + b² = 625

b² = 625 - 49

b² = 576

b = √576

b = 24 ft

The error is the arrangement.

Problem 14 :

How long is the wire that supports the tree?

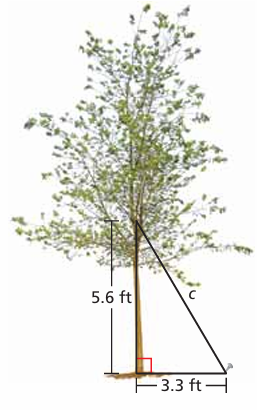
Solution :

c = ?, a = 5.6 ft and b = 3.3 ft

5.6² + 3.3² = c²

31.36 + 10.89 = c²

c² = 42.25

c = √42.25

c = 6.5 ft

So, the required length of the wire is 6.5 ft.

Problem 15 :

The legs of a right triangle have lengths of 28 meters and 21 meters. The hypotenuse has a length of 5x meters. What is the value of x ?

Solution :

c = 5x meter, a = 28 meter and b = 21 meter

28² + 21² = (5x)²

784 + 441 = 25x²

25x² = 1225

x² = 1225/25

x² = 49

x = √49

x = 7

So, the value of x is 7.