FIND UNKNOWN COORDINATE WHEN THE POINTS ARE COLLINEAR

Problem 1 :

Find the values of k if the points A (k + 1, 2k), B (3k, 2k + 3) and C (5k – 1, 5k) are collinear.

Solution :

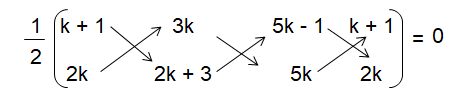
(k+1)(2k+3)-2k(3k)+3k(5k)-(2k+3)(5k-1)+(5k-1)2k- 5k(k+1) = 0

2k² + 5k + 3 - 6k² + 15k² - (10k²+13k-3) + 10k² - 2k - 5k² - 5k = 0

6k² -15k + 6 = 0

Dividing by 3, we get

2k² -5k + 3 = 0

(x - 1)(2x - 3) = 0

x = 0 and x = 3/2

Problem 2 :

Find the value of m if the points (5, 1), (–2, –3) and (8, 2m) are collinear

Solution :

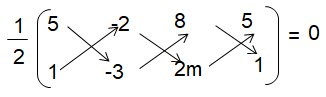
-15-(-2) - 4m - (-24) + 8 - 10m = 0

-15 + 2 - 4m + 24 + 8 - 10m = 0

-14m + 19 = 0

m = 19/4

Problem 3 :

If P (9a–2, –b) divides line segment joining A (3a+1, –3) and B (8a, 5) in the ratio 3 : 1, find the values of a and b.

Solution :

Equating x and y-coordinates, we get

Problem 4 :

If (a, b) is the mid-point of the line segment joining the points

A (10, –6) and B (k, 4) and a – 2b = 18

find the value of k and the distance AB.

Solution :

Comparing the y-coordinates,

b = -1

Comparing x-coordinates,

(10 + k)/2 = a

10 + k = 2a

2a - k = 10  -----(1)

Given a – 2b = 18 ----(2)

Applying the value of b in (2)

a - 2(-1) = 18

a+2 = 18

a = 16

Applying the value of a in (1)

2(16) - k = 10

32 - k = 10

k = 32 - 10

k = 22

Problem 5 :

The line segment joining the points A (3, 2) and B (5,1) is divided at the point P in the ratio 1:2 and it lies on the line 3x – 18y + k = 0. Find the value of k.

Solution :

The line joining the points A and B is divided by the point P, means A, P and B are collinear.

Since the point lies on the line 3x – 18y + k = 0

3(11/3) - 18(5/3) + k = 0

11 - 30 + k = 0

-19 + k = 0

k = 19

Problem 6 :

The center of a circle is (2a, a – 7). Find the values of a if the circle passes through the point (11, –9) and has diameter 10 √2 units.

Solution :

Center of the circle is (2a, a - 7) and it passes through the point (11, -9). By connecting these two points will get a straight line. So, they are collinear.

Distance between these two points will be the radius.

Radius = 10√2/2

= 5√2 units.

(a - 3)(a - 5) = 0

a = 3 and a = 5.

Problem 7 :

If the points A (1, 2), O (0, 0) and C (a, b) are collinear, then

(A) a = b    (B) a = 2b   (C) 2a = b   (D) a = –b

Solution :

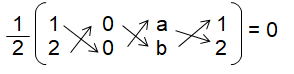
(0 + 0 + 2a) - (0+0+b) = 0

2a - b = 0

2a = b

Problem 8 :

A line intersects the y-axis and x-axis at the points P and Q, respectively. If (2, –5) is the mid-point of PQ, then the coordinates of P and Q are, respectively

(A) (0, – 5) and (2, 0) (B) (0, 10) and (– 4, 0)

(C) (0, 4) and (– 10, 0) (D) (0, – 10) and (4, 0)

Solution :

Let P(a, 0) and Q(0, b) are the points on the x and y-axis respectively.

Midpoint of PQ = (2, -5)

(a + 0)/2 = 2   and (0 + b)/2 =  -5

a = 4 and b = -10

So, the required points are (4, 0) and (0, -10).

Problem 9 :

If P (a/3, 4) is the mid-point of the line segment joining the points Q (– 6, 5) and R (– 2, 3), then the value of a is

(A) – 4      (B) – 12      (C) 12      (D) – 6

Solution :

Midpoint of QR = (a/3, 4)

Equating x-coordinates, we get

-4 = a/3

a = -12