FIND THE VERTEX AND AXIS OF  SYMMETRY OF PARABOLA FROM GRAPH

What is vertex of the parabola ?

If the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic function.

If the parabola opens down, the vertex represents the highest point on the graph, or the maximum value. 

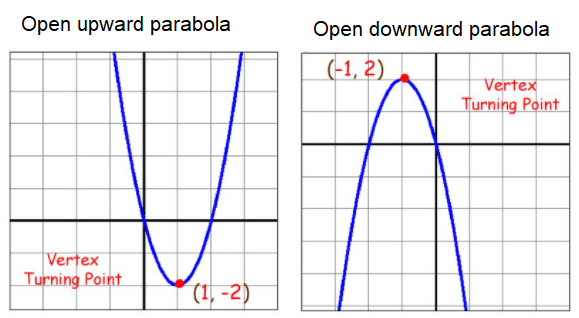
The vertex form of a quadratic polynomial is 

y = a(x - h)² + k

Here (h, k) is vertex.

What is axis of symmetry ?

The axis of symmetry is the vertical line, which divides the parabola into two equal parts.

The axis of symmetry will always pass through the vertex of the parabola.

Axis of symmetry can be found using the formula x = -b/a

Identify the vertex and the axis of symmetry of each parabola.

Problem 1 :

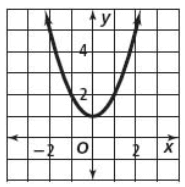
Solution :

While tracing the curve, the minimum point of the parabola is at (0, 1).

Equation of axis of symmetry is at x = 0

Problem 2 :

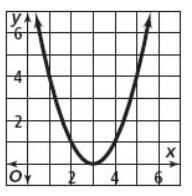
Solution :

The minimum is at (3, 0). So, the vertex is (3, 0).

Axis of symmetry at x = 3.

Problem 3 :

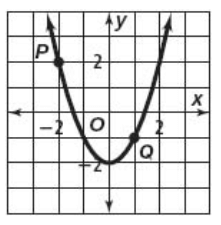
Solution :

The minimum is at (0, -2). So, the vertex is (0, -2).

Axis of symmetry at x = -2.

Graph each function. Label the vertex and the axis of symmetry.

Problem 4 :

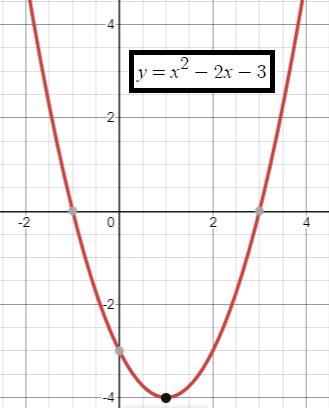
y = x² –2x – 3

Solution :

Finding Vertex :

y = x² –2x – 3

Decomposing coefficient of x as multiple of 2, we get

y = x² –2 ⋅ x ⋅ 1 + 1² - 1² – 3

y = (x - 1)² - 1 – 3

y = (x - 1)² - 4

Vertex (h, k) ==> (1, -4)

a = 1, b = -2 and c = -3

Since a is positive 1, the parabola opens up.

Finding axis of symmetry :

Axis of symmetry x = -b/2a

x = -(-2)/2(1)

x = 1

Problem 5 :

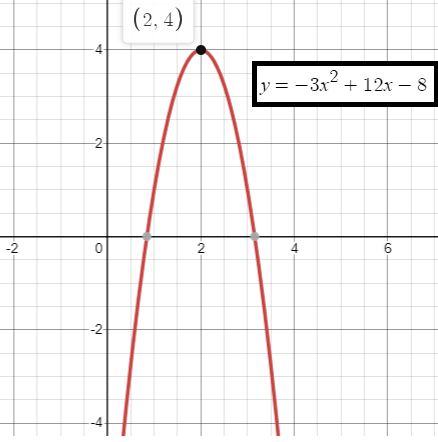
y = -3x² +12x – 8

Solution :

Finding Vertex :

y = -3x² +12x – 8

y = -3[x² -4x] – 8

y = -3[x² - 2⋅ x⋅ 2 + 2² - 2²] – 8

y = -3[(x-2)² - 2²] – 8

y = -3(x-2)² + 12 – 8

y = -3(x - 2)² + 4

Vertex (h, k) ==> (2, 4)

a = -3, b = 12 and c = -8

Since a is negative, the parabola opens down.

Finding axis of symmetry :

Axis of symmetry x = -b/2a

x = -12/2(-3)

x = 12/6

x = 2

Problem 6 :

Tell whether the function f(x) = -4x² - 24x - 19 has a minimum value or a maximum value. Then find the value.

Solution :

f(x) = -4x² - 24x - 19

Sign of leading coeffcient is negative, then the quadratic function will open downward. It may have maximum at vertex.

a = -4, b = -24 and c = -19

x = -b/2a

x = -(-24) / 2(-4)

= -24/8

x = -3

When x = -3

f(3) = -4(-3)² - 24(-3) - 19

= -4(9) + 72 - 19

= -36 + 72 - 19

= 17

So, the maximum is at (-3, 17).

Problem 7 :

The suspension cables between the two tower of the Mackinac bridge in Michigan forn a parabola that can be modelled by y = 0.000098x² - 0.37x + 552, where x and y are measured in feet. What is the height of the cable above the water as its lowest point ?

Solution :

The lowest point of the parabola is at the vertex of the parabola. Finding the x-coordinate of the vertex a = 0.000098 and b = -0.37

x = -(-0.37) / 2(0.000098)

= 1887.7

= 1888

Applying x = 1888 and find the y-coordinate.

 y = 0.000098(1888)² - 0.37(1888) + 552

= 203

The cable is about 203 feet above the water at its lowest point.

Problem 8 :

The function

h(t) = −16t² + 16t

represents the height (in feet) of a horse t seconds after it jumps during a steeplechase.

a. When does the horse reach its maximum height?

b. Can the horse clear a fence that is 3.5 feet tall? If so, by how much?

c. How long is the horse in the air?

Solution :

h(t) = −16t² + 16t

a)

a = -16, b = 16

x = -b/2a

x = -16/2(-16)

= 1/2

= 0.5

It reaches the maximum height in 0.5 minutes.

Maximum height = −16(0.5)² + 16(0.5)

= -16(0.25) + 8

= -4 + 8

= 4 ft

b) Since the maximum height is 4 ft, the horse can clear the height of 3.5 ft.

c) 0 = −16t² + 16t

-16t(t - 1) = 0

t = 0 and t = 1

The horse will be at air in 1 second.

Problem 9 :

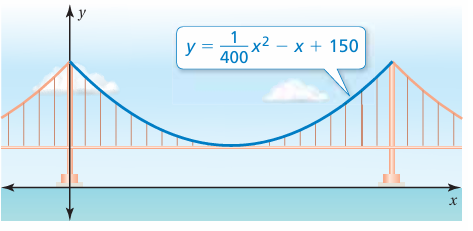
a. How far from each tower shown is the lowest point of the cable?

b. How high is the road above the water?

Solution :

a)

y = (1/400)x² - x + 150

a = 1/400, b = -1 and c = 150

x = -(-1)/2(1/400)

= 1/(1/200)

= 200

200 ft is the lowest point.

b)  y = (1/400)x² - x + 150

Applying x = 200

 y = (1/400)200² - 200 + 150

= 100 - 200 + 150

= 250 - 200

= 50 feet

The function shown represents the height h (in feet) of a firework t seconds after it is launched. The firework explodes at its highest point

a. When does the firework explode?

b. At what height does the firework explode?

Solution :

a) h = -16t² + 128t

a = -16, b = 128 and c = 0

x = -b/2a

x = -128/2(-16)

= 128/32

x = 4

After 4 seconds the firework will explode.

b)  When x = 4

h = -16(4)² + 128(4)

= -16 (16)  + 512

= -256 + 512

= 256 ft