FIND THE VALUE OF X GIVEN A TANGENT TO A CIRCLE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Calculate the length of sides labelled in the circles below. The lines AB and AC are tangents.
Problem 1 :
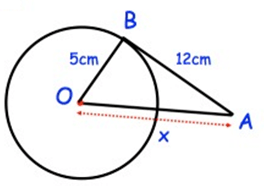
Solution :
Using Pythagorean theorem :
(OA)2 = (OB)2 + (AB)2
x2 = (5)2 + (12)2
x2 = 25 + 144
x2 = 169
x = 13
So, the value of x is13 cm.
Calculate
the length of sides labelled in the circles below. The lines AB and AC are
tangents.
Problem 2 :
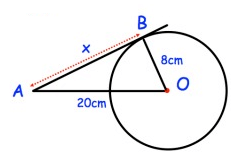
Solution :
Using Pythagorean
theorem :
(AO)2 = (AB)2 + (OB)2
(20)2 = (x)2 + (8)2
400 = x2 + 64
x2 = 400 - 64
x2 = 336
x = 18.330
So, the value of x is18.330 cm.
Problem 3 :
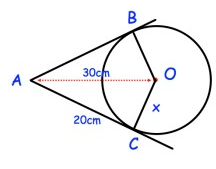
Solution :
Using Pythagorean
theorem :
OA2 = AC2 + OC2
302 = 202 + x2
900 = 400 + x2
x2 = 900 - 400
x2 = 500
x = 10√5
So, the value of x is 22.36 cm.
Calculate the size of x in the circles below. The lines AB and AC are tangents.
Problem 4 :
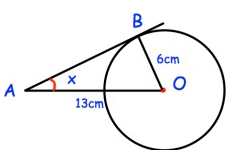
Solution :
sin x = opposite/hypotenuse
= BO/AO
= 6/13
sin x = 0.4615
x = sin -1 (0.4615)
= 27.48
So, the angle is 27.48.
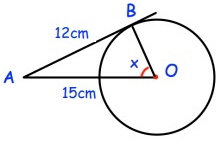
Problem 5 :
Solution :
sin x = opposite/hypotenuse
x = AB/AO
= 12/15
sin x = 0.8
x = sin-1 0.8
= 53.13
So, the angle is 53.13.
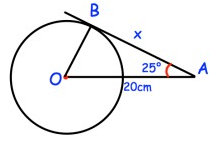
Problem 6 :
Solution :
cos 25º = adjacent/hypotenuse
0.9063 = x/20
x = 0.9063 × 20
x = 18.126
So, the missing side is 18.126 cm.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling