FIND THE VALUE OF GIVEN TRIGONOMETRIC RATIOS

For each triangle, write sin ϴ, cos ϴ and tan ϴ as fractions.

Problem 1 :

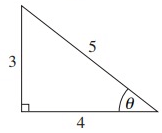
Solution :

From the triangle above,

Hypotenuse = 5

Opposite side = 3

Adjacent side = 4

Finding the value of sin ϴ :

sin ϴ = Opposite side / Hypotenuse

sin ϴ = 3/5

Finding the value of cos ϴ :

cos ϴ = Adjacent side / Hypotenuse

cos ϴ = 4/5

Finding the value of tan ϴ :

tan ϴ = Opposite side / Adjacent side

tan ϴ = 3/4

Problem 2 :

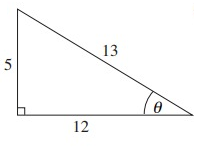
Solution :

From the triangle above,

Hypotenuse = 13

Opposite side = 5

Adjacent side = 12

Finding the value of sin ϴ :

sin ϴ = Opposite side / Hypotenuse

sin ϴ = 5/13

Finding the value of cos ϴ :

cos ϴ = Adjacent side / Hypotenuse

cos ϴ = 12/13

Finding the value of tan ϴ :

tan ϴ = Opposite side / Adjacent side

tan ϴ = 5/12

Problem 3 :

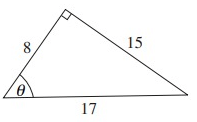
Solution :

From the triangle above,

Hypotenuse = 17

Opposite side = 15

Adjacent side = 8

Finding the value of sin ϴ :

sin ϴ = Opposite side / Hypotenuse

sin ϴ = 15/17

Finding the value of cos ϴ :

cos ϴ = Adjacent side / Hypotenuse

cos ϴ = 8/17

Finding the value of tan ϴ :

tan ϴ = Opposite side / Adjacent side

tan ϴ = 15/8

Problem 4 :

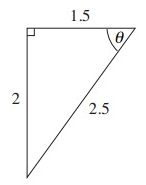
Solution :

From the triangle above,

Hypotenuse = 2.5

Opposite side = 2

Adjacent side = 1.5

Finding the value of sin ϴ :

sin ϴ = Opposite side / Hypotenuse

sin ϴ = 2/2.5

Finding the value of cos ϴ :

cos ϴ = Adjacent side / Hypotenuse

cos ϴ = 1.5/2.5

Finding the value of tan ϴ :

tan ϴ = Opposite side / Adjacent side

tan ϴ = 2/1.5

Problem 5 :

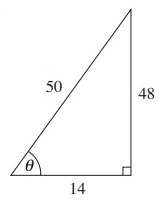
Solution :

From the triangle above,

Hypotenuse = 50

Opposite side = 48

Adjacent side = 14

Finding the value of sin ϴ :

sin ϴ = Opposite side / Hypotenuse

sin ϴ = 48/50

sin ϴ = 24/25

Finding the value of cos ϴ :

cos ϴ = Adjacent side / Hypotenuse

cos ϴ = 14/50

cos ϴ = 7/25

Finding the value of tan ϴ :

tan ϴ = Opposite side / Adjacent side

tan ϴ = 48/14

tan ϴ = 24/7

Problem 6 :

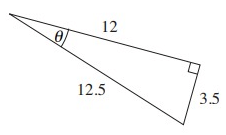
Solution :

Hypotenuse = 12.5

Opposite side = 3.5

Adjacent side = 12

Finding the value of sin ϴ :

sin ϴ = Opposite side / Hypotenuse

sin ϴ = 3.5/12.5

Finding the value of cos ϴ :

cos ϴ = Adjacent side / Hypotenuse

cos ϴ = 12/12.5

Finding the value of tan ϴ :

tan ϴ = Opposite side / Adjacent side

tan ϴ = 3.5/12