FIND THE TURNING POINT OF A PARABOLA
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
What is turning point of the parabola ?
The vertex is the turning point of the parabola.
There are two types of parabola,
(i) Open upward
(ii) Open downward
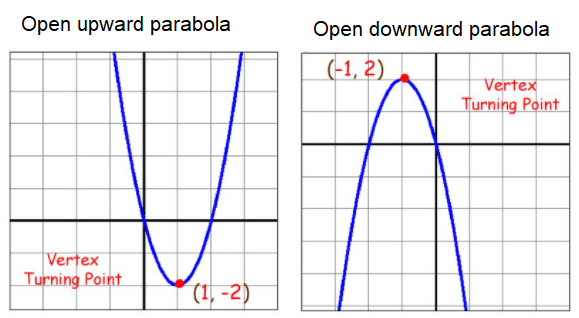
For example,
When we trace the parabola which opens up it will keep on go down after it crosses the turning point or vertex it will go up. That's why we call vertex as turning point.
If the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic function. If the parabola opens down, the vertex represents the highest point on the graph, or the maximum value.
How to find turning point or vertex of the parabola ?
There are two ways to find vertex of the parabola.
(i) Converting the quadratic function into vertex form
y = a(x - h)2 + k
Here (h, k) is the vertex.
(ii) Using formula to find x-coordinate and apply the value of x into the given question to find the value of y.
x = -b/2a
Find the turning point (vertex) of the following quadratic functions.
Problem 1 :
y = x2 - 4x + 2
Solution :
y = x2 - 4x + 2
Using completing the square method,
Step 1 :
Since the coefficient of x2 is 1, writing the coefficient of x as a multiple of 2.
y = x2 - 2⋅x⋅2 + 2
Step 2 :
The middle term looks like 2ab, here b is 2. In order to complete the formula a2 - 2ab, we need b2
So,
y = x2 - 2⋅x⋅2 + 22 - 22 + 2
To balance +b2, we subtract b2.
Step 3 :
y = (x - 2)2 - 4 + 2
Using algebraic identity for first three terms.
y = (x - 2)2 - 2
Here (h, k) is (2, -2).
So, turning point of the parabola is (2, -2)
Method 2 :
Using formula x = -b/2a
y = x2 - 4x + 2
a = 1, b = -4 and c = 2
|
x = -(-4)/2(1) x = 2 |
when x = 2, y = ? y = 22 - 4(2) + 2 y = 4 - 8 + 2 y = 6 - 8 y = -2 |
So, the turning point is (2, -2).
Problem 2 :
y = x2 + 2x - 3
Solution :
y = x2 + 2x - 3
y = x2 + 2⋅x⋅1 + 12 - 12 - 3
y = (x + 1)2 - 12 - 3
y = (x + 1)2 - 4
Turning point is (-1, -4).
Problem 3 :
f(x) = 2x2 + 4
Solution :
f(x) = 2x2 + 4
Factoring 2, we get
f(x) = 2(x2 + 2)
f(x) = 2[(x - 0)2 + 2]
f(x) = 2(x - 0)2 + 4
Turning point (h, k) is (0, 4).
Problem 4 :
f(x) = 2x2 + 4
Solution :
f(x) = -3x2 + 1
Factoring 2, we get
f(x) = -3(x2 - 1/3)
f(x) = 3[(x - 0)2 - (1/3)]
f(x) = 3(x - 0)2 - 1
Turning point (h, k) is (0, -1).
Problem 5 :
Using formula to find vertex of the parabola
f(x) = 2x2 + 8x - 7
Solution :
Here a = 2, b = 8 and c = -7
|
x-coordinate : x = -b/2a x = -8/2(2) x = -8/4 x = -2 |
y-coordinate : y = 2x2 + 8x - 7 When x = - 2 y = 2(-2)2 + 8(-2) - 7 = 2(4) - 16 - 7 = 8 -16 - 7 = -15 |
So, the turning point us (-2, -15).
Problem 6 :
The graph of a quadratic function is shown. Determine which symbols to use to complete the vertex form of the quadratic function. Explain your reasoning.
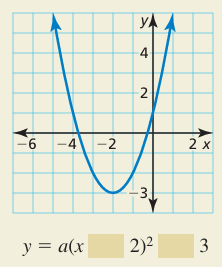
Solution :
By observing the graph, the parabola opens up, then sign of a is positive.
Minimum point is at (-2, -3)
y = a(x - h)2 + k
y = a(x - (-2))2 + (-3)
y = a(x + 2)2 - 3
(0, 1) is one of the point on the parabola.
1= a(0 + 2)2 - 3
1 + 3 = 4a
a = 4/4
a = 1
y = 1(x + 2)2 - 3
y = (x + 2)2 - 3
Problem 7 :
ater fountains are usually designed to give a specific visual effect. For example, the water fountain shown consists of streams of water that are shaped like parabolas. Notice how the streams are designed to land on the underwater spotlights.
Write and graph a quadratic function that models the path of a stream of water with a maximum height of 5 feet, represented by a vertex of (3, 5), landing on a spotlight 6 feet from the water jet, represented by (6, 0).

Solution :
y = a(x - h)2 + k
Vertex is at (3, 5)
y = a(x - 3)2 + 5
Applying the point (6, 0), we get
0 = a(6 - 3)2 + 5
-5 = a(3)2
a = -5/9
y = (-5/9) (x - 3)2 + 5
Problem 8 :
Describe and correct the error in fi nding the vertex of the graph of the function.
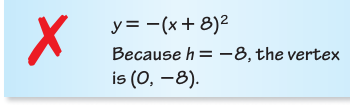
Solution :
y = -(x + 8)2
Comparing the given equation with y = a(x - h)2 + k, the vertex of the parabola is (h, k).
Vertex of the parabola given is (-8, 0). But it is given as (0, -8) and that is the error.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling